Page 114 - 无损检测2024年第五期

包 扬, 等:

基于多项式混沌展开法的涡流无损检测高效元模型辅助探测概率的分析

设阈值, 那么计算出的多项式混沌展开模型就满足
精度要求, 否则需要增加训练点的个数直到模型满
足精度要求为止。

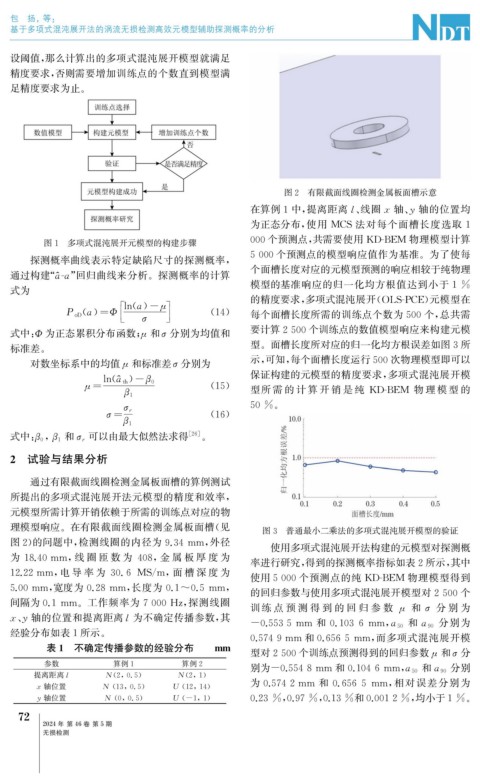
图2 有限截面线圈检测金属板面槽示意

在算例1中, 提离距离l 、 线圈x 轴、 轴的位置均
y

为正态分布, 使用 MCS 法对每个面槽长度选取 1
图1 多项式混沌展开元模型的构建步骤 000个预测点, 共需要使用 KD-BEM 物理模型计算

5000个预测点的模型响应值作为基准。为了使每
探测概率曲线表示特定缺陷尺寸的探测概率,
个面槽长度对应的元模型预测的响应相较于纯物理
通过构建“ a ^ -a ” 回归曲线来分析。探测概率的计算

式为 模型的基准响应的归一化均方根值达到小于 1%
的精度要求, 多项式混沌展开( OLS-PCE ) 元模型在
ln ( a )
- μ
(
=
P oD a ) Φ ( 14 ) 每个面槽长度所需的训练点个数为500个, 总共需

σ
式中: Φ 为正态累积分布函数; 和 σ 分别为均值和 要计算2500个训练点的数值模型响应来构建元模
μ
型。面槽长度所对应的归一化均方根误差如图3所
标准差。
示, 可知, 每个面槽长度运行500次物理模型即可以
对数坐标系中的均值 μ 和标准差 σ 分别为
保证构建的元模型的精度要求, 多项式混沌展开模
)
ln ( a ^ th - β 0
μ= ( 15 ) 型所 需 的 计 算 开 销 是 纯 KD-BEM 物 理 模 型 的
β 1

50% 。
σ r
σ= ( 16 )
β 1

式中: , 和 σ r 可以由最大似然法求得 [ 26 ] 。
β 0 β 1
2 试验与结果分析
通过有限截面线圈检测金属板面槽的算例测试
所提出的多项式混沌展开法元模型的精度和效率,
元模型所需计算开销依赖于所需的训练点对应的物
理模型响应。在有限截面线圈检测金属板面槽( 见 图3 普通最小二乘法的多项式混沌展开模型的验证
图2 ) 的问题中, 检测线圈的内径为 9.34mm , 外径

使用多项式混沌展开法构建的元模型对探测概

为 18.40mm , 线 圈 匝 数 为 408 , 金 属 板 厚 度 为
率进行研究, 得到的探测概率指标如表2所示, 其中

12.22mm , 电 导 率 为 30.6 MS / m , 面 槽 深 度 为 使用5000个预测点的纯 KD-BEM 物理模型得到

5.00mm , 宽度为 0.28mm , 长度为 0.1~0.5mm , 的回归参数与使用多项式混沌展开模型对2500个

间隔为0.1mm 。工作频率为 7000Hz , 探测线圈
训练 点 预 测 得 到 的 回 归 参 数 μ 和 σ 分 别 为
x 、 轴的位置和提离距离 l 为不确定传播参数, 其 分别为
y
-0.5535mm 和 0.1036 mm , a 50 和 a 90
经验分布如表1所示。
0.5749mm 和0.6565mm , 而多项式混沌展开模
表1 不确定传播参数的经验分布 mm 型对2500个训练点预测得到的回归参数 和 σ 分

参数 算例1 算例2 μ 分别
别为-0.5548mm 和0.1046mm , a 50 和a 90
提离距离 l N ( 2 , 0.5 ) N ( 2 , 1 )
为 0.5742mm 和 0.6565 mm , 相对误差分别为
x 轴位置 N ( 13 , 0.5 ) U ( 12 , 14 )

y 轴位置 N ( 0 , 0.5 ) U ( -1 , 1 ) 0.23% , 0.97% , 0.13%和0.0012% , 均小于1% 。
2
7
2024年 第46卷 第5期
无损检测