Page 71 - 无损检测2024年第十二期

黄梓琦，等：

基于改进模量比寻根算法的黏弹性多层空心圆柱超声导波特性分析

A mj =0 （11）
，
22
式（10）表示超声导波纵向模态，式（11）表示
超声导波扭转模态。通过求解式中的复波数k和角
频率ω，即可获得相应模态的频散曲线和衰减曲线。

2 改进的寻根算法

不同于参考文献[18-19]将各向异性层状复合材
料的频散方程求解问题转化为特征值问题，文章利
图 2 单变量函数示意
用迭代寻根算法求解方程。尽管常用的迭代寻根算
法，如二分法和牛顿-拉夫逊法，已被证明适用于求 所以，比值|f (c)|/|f (x )|和|f (d)|/|f (x )|都为无穷大。
2
2
解弹性材料的频散特征方程，但在处理黏弹性材料 因此，必然存在某个有限值P，使得
时存在困难。黏性的引入使得频散特征方程具有复
波数根，在频率-复波数空间中使用传统的二分法求
（13）
根存在局限性。牛顿-拉夫逊法要求目标函数具有
二阶连续可微性，并且需要计算目标函数的Hessian
矩阵的逆，计算量巨大。为了克服这些限制，文章提 此处的有限值P可以作为一个阈值，用于判断
出了改进的模量比寻根算法，并实现基于LOPE方
所找到的极小值点是否为零点。
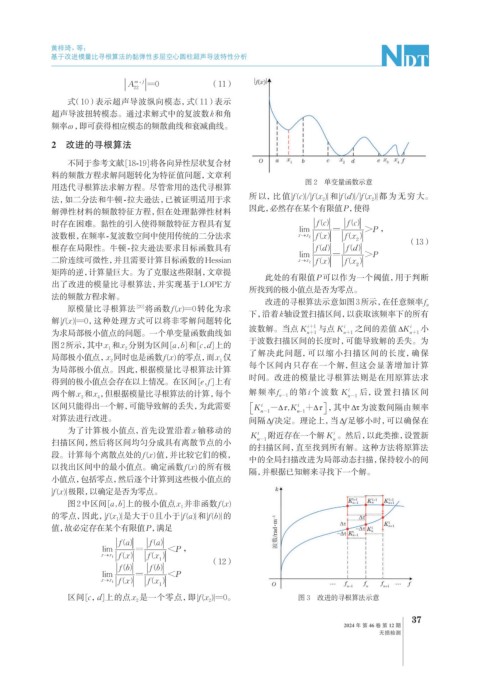
法的频散方程求解。 改进的寻根算法示意如图3所示，在任意频率f
原模量比寻根算法 [20] 将函数f (x)=0转化为求 n
下，沿着k轴设置扫描区间，以获取该频率下的所有
解|f(x)|=0，这种处理方式可以将非零解问题转化
波数解。当点 K i +1 与点 K i 之间的差值 K i 小
∆
为求局部极小值点的问题。一个单变量函数曲线如 n +1 n +1 n +1
图2所示，其中x 和x 分别为区间[a,b]和[c,d]上的 于波数扫描区间的长度时，可能导致解的丢失。为
1
2
局部极小值点，x 同时也是函数f(x)的零点，而x 仅 了解决此问题，可以缩小扫描区间的长度，确保
1
2
为局部极小值点。因此，根据模量比寻根算法计算 每个区间内只存在一个解，但这会显著增加计算
时间。改进的模量比寻根算法则是在用原算法求
得到的极小值点会存在以上情况。在区间[e,f ]上有
两个解x 和x ，但根据模量比寻根算法的计算，每个 解频率f n-1 的第i个波数 K n i 后，设置扫描区间
3 4 -1
区间只能得出一个解，可能导致解的丢失，为此需要  i n - K ∆ , τ  n i − + K ∆ τ   ，其中∆τ为波数间隔由频率
1
-1
对算法进行改进。 间隔∆f决定。理论上，当∆f足够小时，可以确保在
为了计算极小值点，首先设置沿着x轴移动的 K i 附近存在一个解 K 。然后，以此类推，设置新
i
扫描区间，然后将区间均匀分成具有离散节点的小 n -1 n
的扫描区间，直至找到所有解。这种方法将原算法
段。计算每个离散点处的f (x)值，并比较它们的模，
中的全局扫描改进为局部动态扫描，保持较小的间
以找出区间中的最小值点。确定函数f (x)的所有极
隔，并根据已知解来寻找下一个解。
小值点，包括零点，然后逐个计算到这些极小值点的
|f (x)|极限，以确定是否为零点。
图2中区间[a,b]上的极小值点x 并非函数f (x)
1
的零点，因此，f (x )|是大于0且小于|f (a)|和|f(b)|的
|
1
值，故必定存在某个有限值P，满足

（12）

区间[c，d]上的点x 是一个零点，即|f (x )|=0。 图 3 改进的寻根算法示意
2
2
37
2024 年 第 46 卷 第 12 期
无损检测