Page 97 - 无损检测2024年第八期
P. 97
吴 伟,等:
车轴压装界面微动磨损尺寸的非线性检测
图 7 不同时刻应力第二主不变量与边界声压图
图7(c),(d)展示了边界一、边界二的压力变化。 明显,而频域信号,信号在基波(1.5 MHz)、二次谐波
入射波透过边界一在4.427×10 s时边界压力值最 (3 MHz)中均产生峰值且存在差异。验证了非线性系
−6
小,在边界二上1.956×10 s时边界压力值最小。边 数对车轴压装界面微动磨损尺寸定量评估的可行性。
−5
界一与边界二的距离为90 m,由此可计算出折射纵
波速度为5 947 m · s ,实际纵波速度与预设超声纵 3 有限元仿真结果分析
−1
波速度(5 928 m · s )相近。由于横波波速远低于纵 3.1 超声透射信号频域分析
−1
波波速,横波易被噪音淹没,无法准确测量。故根据 在不同微动磨损长度、深度及压装力下的频域
图7(b) 可计算横波大约波速,通过图中点的位置与 信号如图 9 所示,可见透射波在 1.5 MHz和 3 MHz
传播时间,可计算得横波波速为3 470 m · s 。与实 位置处均存在幅值,非线性效应明显。如图9(a) ,(b)
−1
际横波波速(3 260 m · s )存在误差,但考虑人为 所示,随着微动磨损长度的增加,透射波的基波幅值
−1
读取数据误差以及具体点位置估读误差等(误差在 逐渐减小、二次谐波的幅值逐渐增大。如图9(c) ,(d)
10%以内),故可认定该模型横波与纵波波速验证均 所示,随着微动磨损深度的增加,透射波的基波幅值
正确。 逐渐减小、二次谐波的幅值逐渐增大。如图9(e) ,(f)
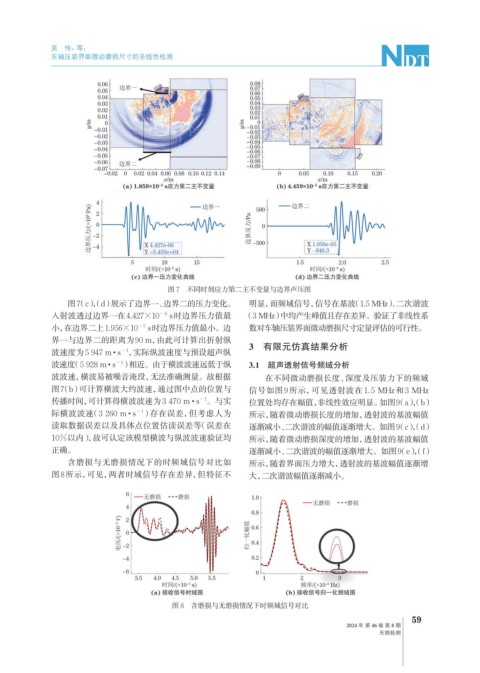
含磨损与无磨损情况下的时频域信号对比如 所示,随着界面压力增大,透射波的基波幅值逐渐增
图8所示,可见,两者时域信号存在差异,但特征不 大,二次谐波幅值逐渐减小。
图 8 含磨损与无磨损情况下时频域信号对比
59
2024 年 第 46 卷 第 8 期
无损检测