Page 77 - 无损检测 2021年第六期

蒋 菲, 等:

基于 CEEMDAN 能量熵和 SVM 的风电叶片缺陷检测

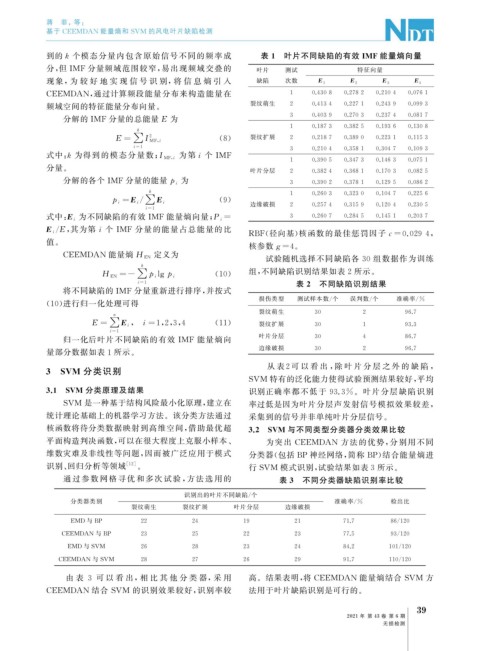
到的k 个模态分量内包含原始信号不同的频率成 表 1 叶片不同缺陷的有效IMF 能量熵向量
分, 但IMF 分量频域范围较窄, 易出现频域交叠的 叶片 测试 特征向量
现 象, 为 较 好 地 实 现 信 号 识 别, 将 信 息 熵 引 入 缺陷 次数 E 1 E 2 E 3 E 4

CEEMDAN , 通过计算频段能量分布来构造能量在 1 0.4308 0.2782 0.2104 0.0761

裂纹萌生 2 0.4134 0.2271 0.2439 0.0993
频域空间的特征能量分布向量。

分解的IMF 分量的总能量 E 为 3 0.4039 0.2703 0.2374 0.0817

1 0.1873 0.3825 0.1936 0.1308
k
2
E = ∑ I MF , i ( 8 ) 裂纹扩展 2 0.2187 0.3890 0.2231 0.1153

i =1
3 0.2104 0.3581 0.3047 0.1093
式中: k 为得到的模态分量数; I MF , i 为第i 个 IMF
1 0.3905 0.3473 0.1463 0.0751
分量。 叶片分层 2 0.3824 0.3681 0.1703 0.0825

为
分解的各个IMF 分量的能量 p i 3 0.3902 0.3781 0.1295 0.0862
k
1 0.2603 0.3230 0.1047 0.2256
/ ( 9 )
p i =E i ∑ E i 边缘破损 2 0.2574 0.3159 0.1204 0.2305
i = 1

式中: E i 为不同缺陷的有效IMF 能量熵向量; P i= 3 0.2607 0.2845 0.1451 0.2037
E i E , 其为第i 个 IMF 分量的能量占总能量的比
/
RBF ( 径向基) 核函数的最佳惩罚因子c=0.0294 ,
值。
核参数 g=4 。
定义为
CEEMDAN 能量熵 H EN 试验随机选择不同缺陷各 30 组数据作为训练
k
组, 不同缺陷识别结果如表 2 所示。
H EN =- ∑ p i l gp i ( 10 )
i =1 表 2 不同缺陷识别结果
将不同缺陷的IMF 分量重新进行排序, 并按式
损伤类型 测试样本数 / 个 误判数 / 个 准确率 / %
( 10 ) 进行归一化处理可得
裂纹萌生
n 30 2 96.7
E = ∑ E i i= 1 , 2 , 3 , 4 ( 11 ) 裂纹扩展 30 1 93.3
,
i = 1
归一化后叶片不同缺陷的有效 IMF 能量熵向 叶片分层 30 4 86.7
边缘破损 30 2 96.7
量部分数据如表 1 所示。
3 SVM 分类识别 从 表2可 以 看 出 , 除 叶 片 分 层 之 外 的 缺 陷 ,
SVM 特有的泛化能力使得试验预测结果较好, 平均
3.1 SVM 分类原理及结果 识别正确率都不低于 93.3% 。叶片分层缺陷识别
SVM 是一种基于结构风险最小化原理, 建立在 率过低是因为叶片分层声发射信号模拟效果较差,
统计理论基础上的机器学习方法。该分类方法通过 采集到的信号并非单纯叶片分层信号。
核函数将待分类数据映射到高维空间, 借助最优超 3.2 SVM 与不同类型分类器分类效果比较
平面构造判决函数, 可以在很大程度上克服小样本、 为突出 CEEMDAN 方法的优势, 分别用不同
维数灾难及非线性等问题, 因而被广泛应用于模式 分类器( 包括 BP 神经网络, 简称 BP ) 结合能量熵进
识别、 回归分析等领域 [ 12 ] 。 行 SVM 模式识别, 试验结果如表 3 所示。
通 过 参 数 网 格 寻 优 和 多 次 试 验 , 方 法 选 用 的 表 3 不同分类器缺陷识别率比较
识别出的叶片不同缺陷 / 个
分类器类别 准确率 / % 检出比
裂纹萌生 裂纹扩展 叶片分层 边缘破损
EMD 与 BP 22 24 19 21 71.7 86 / 120
CEEMDAN 与 BP 23 25 22 23 77.5 93 / 120
EMD 与 SVM 26 28 23 24 84.2 101 / 120
CEEMDAN 与 SVM 28 27 26 29 91.7 110 / 120
由 表 3 可 以 看 出, 相 比 其 他 分 类 器, 采 用 高。结果表明, 将 CEEMDAN 能量熵结合 SVM 方
CEEMDAN 结合 SVM 的识别效果较好, 识别率较 法用于叶片缺陷识别是可行的。

9
3
2021 年 第 43 卷 第 6 期

无损检测