Page 79 - 无损检测2023年第四期

丁 妍, 等:

基于三次 B样条小波变换和 Cann y 算法的火焰边缘检测算法

平均灰度越接近。
的像
设T A 为图像平均灰度, k A 为灰度为 T A
的分割面积内的像素
素个数, M T 是以灰度为 T A
数, 需要分割的面积图像复杂度可表示为
( /
C T =-M T lo gk A N ) ( 11 )
A
为中心, 在以
目标与背景的分割阈值可以 T A
b 个灰度为半径的邻域内进行最佳阈值的搜索, 即
C T

b= 1- A · aL ( 12 )
Nlo g N
式中: a 为比例系数, 取值区间为[ 0.05 , 0.15 ]; N 为
总的像素数。

图2 梯度计算模板 最终灰度级在( T A-b , T A+b ) 之内搜索, Otsu
算法的运行速度得到了提高。
, 。
Δ 3 Δ 4
求幅值方向时, 将4个方向上的梯度分量合成 2.3 融合算法
融合算法具体步骤如下: ① 对火焰图像进行基
到水平和垂直两个方向上, 经运算, 则总梯度方向为
于三次 B样条小波变换和 Cann y 算法的边缘检测,
2 2
Δ 2+ Δ 3- Δ 4 得到检测结果, 对两个边缘检测结果分别进行小波
2 2
θ= arctan ( 8 ) 分解处理, 得到各自算法的高、 低频分量。 ② 采用
2
Δ 1+ Δ 3- 2 绝对值极大法对高频分量进行融合, 同时采用均值
Δ 4

2 2

2.2.2 Ostu算法确定阈值 法对低频分量进行融合, 然后对融合后的高、 低频分
选取 Ostu 算法计算高低阈值, 提高算法的自 量进行小波逆变换重构。
和
适应性。将像素的灰度值分成两类, 分别是 C 1 3 仿真试验结果及分析
的
C 2 C 1 表示大于高阈值, C 1
, 表示小于高阈值, C 2
3.1 仿真试验结果
。
均值为 m 1 C 2 , 整幅图像均值为m G
, 的均值为m 2
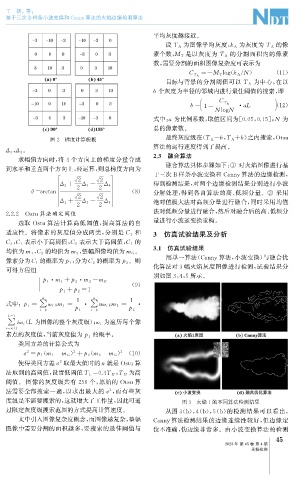
用单一算法( Cann y 算法, 小波变换) 与融合优
的概率为 的概率为 。则
像素分为C 1 , 分为C 2
p 1 p 2 化算法对3幅火焰灰度图像进行检测, 试验结果分
可得方程组
别如图3 , 4 , 5所示。
· ·
p 1 m 1+p 2 m 2=m G ( 9 )
p 1+p 2= 1
n n
1 1
;
式中: p i = ∑ ω 1 m 1 = · ∑ nω i m 2 = ·
;
i = 0 p 1 i = 0 p 2
L - 1
(
∑ iω i L 为图像的整个灰度级); ω i 为遍历每个像
i = n + 1
素点的灰度值, 当前灰度值为 的概率。
p 1
类间方差的计算公式为
2
2
2 ( ) ( ) ( 10 )
σ = p 1 m 1-m G +p 2 m 2-m G
使得类间方差 σ 取最大值时的 n 就是 Ostu算
2
, 为高
法取到的高阈值, 设置低阈值T L= 0.4T H T H
阈值。 图像的灰度级共有 256 个, 原始的 Otsu 算
法需要全部搜索一遍, 以求出最大的σ , 而有些灰
2
度级是不需要搜索的, 这就增大了工作量, 因此可通 图3 火焰1的不同算法检测结果
过限定灰度级搜索范围的方式提高计算速度。 从图3 ( b ), 4 ( b ), 5 ( b ) 的检测结果可以看出,
文中引入图像复杂度概念, 而图像越复杂, 整幅 Cann y 算法检测结果的边缘连续性较好, 但边缘定
图像中需要分割的面积越多, 要搜索的最佳阈值与 位不准确, 伪边缘非常多。由小波变换算法的检测
5
4
2023年 第45卷 第4期
无损检测