Page 43 - 无损检测2023年第三期

韩 芳, 等:

基于压电阻抗法的带裂缝木梁损伤检测

表2 压电片的性能参数

-12 2 -1
压电柔度系数( ×10 m · N )
S 11 = S 22 S 33 S 12 S 13 = S 23 S 44 = S 55 S 66
=16.50 =20.60 =-4.79 =-8.50 =42.60 =42.58
压电应变常数、 密度 /
相对介电常数
-12 -1 -3
( ×10 mV ) ( k g · m )
ε r11 = ε r2 ε r33 d 31 = d 32 d 33 d 24 = d 15
7750

=3130 =1700 =-195 =450 =650
步数为801 , 进行谐响应分析。计算得到带裂缝损
伤木梁的阻抗数值曲线如图7所示。带裂缝损伤木

梁的损伤指数( 150~300kHz ) 如图8所示。

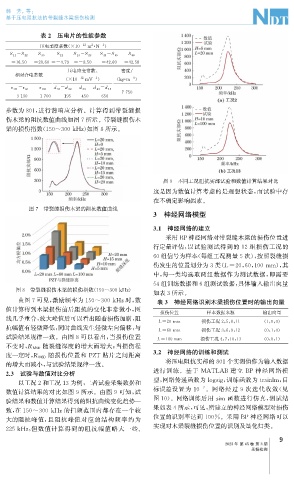
图9 不同工况阻抗实部试验和数值计算结果对比
这是因为数值计算考虑的是理想状态, 而试验中存
在不确定影响因素。
图7 带裂缝损伤木梁的阻抗数值曲线
3 神经网络模型

3.1 神经网络的建立
采用 BP神经网络对带裂缝木梁的损伤位置进
行定量评估, 以试验测试得到的 12 组损伤工况的
60组信号为样本( 每组工况测量5次), 按照裂缝损
伤发生的位置划分为3类( L=20 , 60 , 100mm ), 其

中, 每一类均选取两组数据作为测试数据, 即需要
54组训练数据和6组测试数据, 具体输入输出向量

图8 带裂缝损伤木梁的损伤指数( 150~300kHz )
如表3所示。

由图7可见, 激励频率为150~300kHz时, 数 表3 神经网络识别木梁损伤位置时的输出向量
值计算得到木梁损伤前后阻抗的变化非常微小, 图
损伤位置 样本数据来源 输出向量
线几乎重合, 放大峰值后可以看出随着损伤加剧, 阻
L=20mm 损伤工况2 , 5 , 8 , 11 ( 1 , 0 , 0 )
抗幅值有轻微降低, 同时曲线发生轻微左向偏移, 与
L=60mm 损伤工况3 , 6 , 9 , 12 ( 0 , 1 , 0 )
试验结果规律一致。由图8可以看出, 当损伤位置
L=100mm 损伤工况4 , 7 , 10 , 13 ( 0 , 0 , 1 )
随裂缝深度的增大而增大; 当损伤程
不变时, R MSD
随损伤位置和 PZT 贴片之间距离 3.2 神经网络的训练和测试
度一定时, R MSD
将压电阻抗实部的801个实测值作为输入数据
的增大而减小, 与试验结果规律一致。
进行训练。基于 MATLAB 建立 BP 神经网络模
2.3 试验与数值对比分析
,
以工况2和工况13为例, 二者试验采集数据和 型, 网络传递函数为lo g si g 训练函数为trainlm , 目
标误差设置为 10 。网络经过 9 次迭代收敛( 见
-7
数值计算结果的对比如图9所示。由图9可知, 试
图10 )。网络训练后用 sim 函数进行仿真, 测试结
验结果和数值计算结果得到的阻抗曲线变化趋势一
果如表4所示, 可见, 所建立的神经网络模型对损伤
致, 在150~300kHz的扫频范围内都存在一个较

位置的识别率达到100% 。采用 BP 神经网络可以
大的阻抗峰值, 且阻抗峰值对应的结构频率约为
实现对木梁裂缝损伤位置的识别及量化归类。
225kHz , 但数值计算得到的阻抗幅值略大一些。
9
2023年 第45卷 第3期
无损检测