Page 48 - 无损检测2023年第三期

邱 巧, 等:

基于 ECPT 的拉应力对铁磁材料缺陷量化影响的仿真分析

直缺陷, 垂直于应力方向的缺陷为横向缺陷), 缺陷 状态下对应的相对磁导率分布情况。为进一步量化

深度( D ) 为0.2 , 0.4 , 0.6 , 0.8 , 1.0mm 。拉伸试件材 分析, 表2为不同方向、 不同深度缺陷在不同拉应力
料 Q235钢的相关参数如表1所示。 作用下的最大相对磁导率( ) 数据, 图6 ( a ),( b ) 为
μ max
表1 Q 235材料参数 横向缺陷的 与应力和缺陷深度之间的关系曲
μ max
材料参数 数值 线, 可见横向缺陷的 μ max 随着弹性拉应力的增大而
泊松比 0.3 增大, 且一定应力作用下铁磁材料的 μ max 与横向缺
杨氏模量 / Pa 2×10 11 陷深度成正比。图6 ( c ),( d ) 为竖直缺陷的 与应
μ max
-3
密度 /( g · cm ) 7.85 力和深度之间的关系曲线, 可以看出不同深度竖直缺
屈服强度 / MPa 235
陷的 随着弹性拉应力的增大而增大, 但相同应
-1 ) μ max
电导率 /( MS · m 8.41
力状态下同一深度竖直缺陷的 变化不大。
相对介电常数 1 μ max
表2 不同深度缺陷试件在应力作用下的
未受力状态相对磁导率 500
最大相对磁导率
-1 -1 44.5
导热系数 /( W · m · K )
-1 -1 应力 / 横向缺陷深度 / mm
恒压热容 /( J · k g · K ) 475
MPa 0.2 0.4 0.6 0.8 1.0
2.2 应力对不同深度缺陷的应力分布与相对磁导
10 516.3 518.1 522.4 524.8 530.1
率影响
20 535.1 539.3 549.6 555.6 569.6
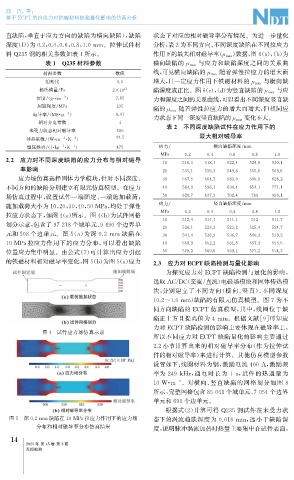
应力场仿真选择固体力学模块, 针对不同深度、 30 557.5 564.7 583.9 595.9 626.2
不同方向的缺陷分别建立有限元仿真模型。在应力 40 584.9 596.1 630.4 654.1 771.1
场仿真过程中, 设置试件一端固定、 一端施加载荷, 50 620.7 637.3 702.4 760 999.1

施加载荷大小为10 , 20 , 30 , 40 , 50MPa , 均处于弹性 应力 / 竖直缺陷深度 / mm
MPa 0.2 0.4 0.6 0.8 1.0
拉应力状态下, 如图4 ( a ) 所示。图4 ( b ) 为试件网格
10 512.4 511.1 511.1 512 511.7

划分示意, 包含了97218个域单元、 9490个边界单

20 526.1 523.3 523.2 525.4 524.7
元和508个边单元。图 5 ( a ) 为深 0.2mm 缺陷在 30 541.4 536.9 536.7 540.3 539.2

10MPa拉应力作用下的应力分布, 可以看出缺陷 40 558.9 552.2 551.8 557.4 555.5
位置应力集中明显。由公式( 7 ) 可计算出应力引起 50 579.2 569.6 569.1 577.2 574.3
的铁磁材料相对磁导率变化, 图5 ( b ) 为图5 ( a ) 应力 2.3 应力对 ECPT缺陷检测与量化影响
为探究应力对 ECPT 缺陷检测与量化的影响,
选取 AC / DC ( 交流 / 直流) 电磁场模块和固体传热模
块, 分别建立了不同方向( 横向、 竖直)、 不同深度

( 0.2~1.0mm ) 缺陷的有限元仿真模型。图7为不
同方向缺陷的 ECPT 仿真模型, 其中, 线圈位于缺

陷正上方且提离值为 4mm 。根据文献[ 9 ] 可知应
力对 ECPT 缺陷检测的影响主要体现在磁导率上,
图4 试件应力场仿真示意
所以不同应力对 ECPT 缺陷量化的影响主要通过
2.2小节计算出来的相对磁导率分布( 作为拉伸试
件的相对磁导率) 来进行计算。其他仿真模型参数

设置如下: 线圈材料为铜, 激励电流 400A , 激励频

率为 249kHz , 通电时长为 1s , 试件的热通量为

-2
10W · m 。对横向、 竖直缺陷的网格划分如图 8

所示, 完整网格包含85041个域单元、 7054个边界
单元和691个边单元。
根据式( 2 ) 计算可得 Q235 钢试件在未受力状
图5 深0.2mm 缺陷在10MPa拉应力作用下的应力场 态下的涡流趋肤深度为 0.016mm , 远小于缺陷深

分布和相对磁导率分布仿真结果
度, 说明脉冲涡流加热时热量主要集中在试件表面,
4
1
2023年 第45卷 第3期
无损检测