Page 42 - 无损检测2023年第三期

韩 芳, 等:

基于压电阻抗法的带裂缝木梁损伤检测

图3 现场试验装置外观
次, 取平均值以减少测量误差。此外, 为降低试验环
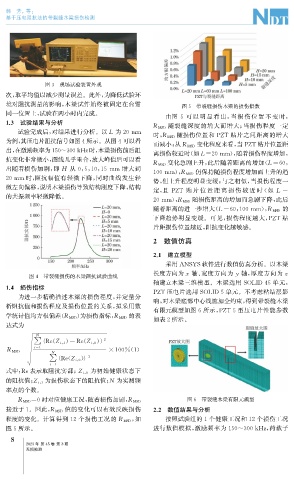
境对阻抗测量的影响, 木梁试件始终被固定在台钳 图5 带裂缝损伤木梁的损伤指数

同一位置上, 试验在两小时内完成。
由图 5 可以明显看出, 当 损 伤 位 置 不 变 时,
1.3 试验结果与分析 随裂缝深度的增大而增大; 当损伤程度一定
R MSD

试验完成后, 对结果进行分析。以L 为20mm 随损伤位置和 PZT 贴片之间距离的增大
时, R MSD
为例, 其压电片阻抗信号如图4所示。从图4可以看
而减小; 从R MSD 变化程度来看, 当 PZT 贴片位置距
出, 在激励频率为150~300kHz 时, 木梁损伤前后阻

离损伤较近时( 如L=20mm ), 随着损伤程度增加,
抗变化非常微小, 图线几乎重合, 放大峰值后可以看
变化急剧上升, 此后随着距离的增加( L=60 ,
R MSD

出随着损伤加剧, 即 H 从 0 , 5 , 10 , 15mm 增大到
100mm ), R MSD 仍保持随损伤程度增加而上升的趋

20mm 时, 阻抗幅值有轻微下降, 同时曲线发生轻 势, 但上升程度明显变缓; 与之相似, 当损伤程度一
微左向偏移, 说明木梁损伤导致结构刚度下降, 结构
定, 且 PZT 贴 片 位 置 距 离 损 伤 较 近 时 ( 如 L =
的共振频率轻微降低。 随损伤距离的增加而急剧下降, 此后
20mm ), R MSD

的
随着距离的进一步增大( L=60 , 100mm ), R MSD
下降趋势明显变缓。可见, 损伤程度越大, PZT 贴
片距损伤位置越近, 阻抗变化越敏感。
2 数值仿真
2.1 建立模型
采用 ANSYS软件进行数值仿真分析。以木梁
长度方向为x 轴、 宽度方向为 轴, 厚度方向为z
图4 带裂缝损伤的木梁阻抗试验曲线 y

轴建立木梁三维模型。木梁选用 SOLID45 单元,
1.4 损伤指标 PZT 压电片选用 SOLID5单元。不考虑粘结层影

为进一步精确描述木梁的损伤程度, 并定量分
响, 对木梁底部中心线施加全约束, 得到带裂缝木梁
析阻抗值和损伤程度及损伤位置的关系, 拟采用数
有限元模型如图6所示, PZT-5型压电片性能参数
的表
学统计值均方根偏差( R MSD ) 为损伤指标, R MSD
如表2所示。
达式为
N
)
)
∑ Re ( Z i , 1 -Re ( Z i , 0 2
i = 1
R MSD= N ×100% ( 1 )
)
∑ Re ( Z i , 0 2
i = 1
为初始健康状态下
式中: Re表示取阻抗实部; Z i , 0
为损伤状态下的阻抗值; N 为实测频
的阻抗值; Z i , 1
率点的个数。
图6 带裂缝木梁有限元模型
R MSD=0时对应健康工况, 随着损伤加剧, R MSD
值的变化可以有效反映损伤
接近于1 。因此, R MSD 2.2 数值结果与分析
, 如 按照试验组的1个健康工况和12个损伤工况
程度的变化。计算得到 12 个损伤工况的 R MSD
图5所示。 进行数值模拟, 激励频率为150~300kHz , 荷载子
8
2023年 第45卷 第3期
无损检测