Page 47 - 无损检测2023年第三期

邱 巧, 等:

基于 ECPT 的拉应力对铁磁材料缺陷量化影响的仿真分析

f
式中: 为激励电流的频率; 为趋肤深度。 B m - B m -8λ m μ 0 μ T B m σ
ξ
2
2
4
由焦耳定律可知, 产生的涡流会在材料内部由 μ σ = ( 8 )
4 μ 0 σλ m
电能转化为热量, 即 -7 -1
式中: 为真空磁导率, 取值为4π×10
μ 0 H · m ;
μ f 为材料初始未受力状态下的初始相对磁导率;
2 ( 3 ) μ T
Q ~I coil
δ
μ σ 为试件受到应力作用时材料的相对磁导率; B m
为材料的饱和磁感
式中:“ ~ ” 表示成正比关系; Q 为产生的热量; I coil
为材料的饱和磁感应强度; λ σ
为线圈中的电流大小。 应系数。
1.1.2 缺陷处热流的传导机理 文章探究的拉伸试件材料为 Q235 钢, 其材料
由于 ECPT 检测存在趋肤效应, 铁磁材料的涡
电磁属性参数为: 为500 ; B m 为2.5T ; λ σ 为5×
μ T
流热成像检测可以视为表面加热过程。当缺陷体积 10 。 Q235钢的力磁函数对应的磁导率与拉应力
-6
深度比大于2时, 横向热传递导致的“ 模糊效应” 对 的关系如图2所示。
纵向热传递影响较小, 可以忽略不计, 从而其热传导
微分方程可简化为一维模型
2
∂T ∂T
α 2 = ( 4 )
∂x ∂t
式中: T 为温度; x 为横坐标; α 为热扩散率。
PARKER 等 [ 12 ] 通过简化 CARSLAW 等 [ 13 ] 提
出的一维解析模型得到反射模式下无缺陷区域的温
度变化T ( t ) 为
refl
∞ 2 2 图2 Q235钢磁导率随拉应力的变化关系
Q nπ

refl
T ( t ) = 1+2 ∑ ex p- 2 αt ( 5 )

ρ C p L n= 1 L 由图2可以看出, 拉应力不大于 249 MPa时,

ρ
式中: L 为试件的厚度;, C p 分别为材料的密度和 试件磁导率随着应力的增大而增大; 拉应力超过
热容量。
249MPa时, 试件磁导率随着应力的增大而减小。
缺陷区域的温度变化T d t 可以表示为
refl
()
结合公式( 3 ) 可以看出, 涡流产生的热量与磁导率呈
∞ 2 2
Q nπ 正相关。综上可以得出: 弹性拉应力作用下, 铁磁材
refl

T d t = 1+2 ∑ ex p- 2 αt ( 6 )
()

ρ C p L r n= 1 L r 料涡流生热随着拉应力的增大而增加。
为缺陷区域的剩余厚度, 小于试件的整体
式中: L r
厚度L 。 2 仿真模型的建立与分析
公式( 5 ),( 6 ) 说明缺陷区域的温度变化和无缺
2.1 仿真对象
陷处的温度变化与表面施加的热量成正比, 与剩余
采用 COMSOLMulti p h y sics5.6软件进行仿真
厚度成反比, 即在相同热量的情况下, 缺陷区域边沿
模型的建立与分析, 仿真对象为铁磁性拉伸试件, 包
的温度会高于无缺陷区域的温度。因此, 缺陷区域
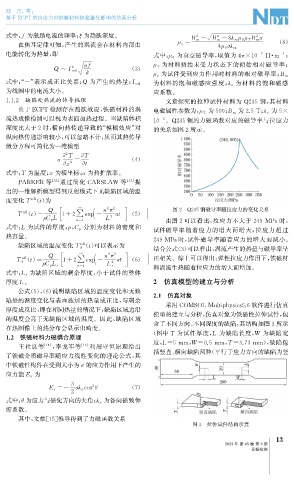
含了不同方向、 不同深度的缺陷, 其结构如图3所示
在热图像上的热分布会显示出畸变。
( 图中T 为试件厚度, L 为缺陷长度, W 为缺陷宽
1.2 铁磁材料力磁耦合原理 度, L=5mm , W =0.5mm , T=3.73mm ), 缺陷包

王社良等 [ 14 ] , 李龙军等 [ 15 ] 利用守恒原理给出 括竖直、 横向缺陷两种( 平行于应力方向的缺陷为竖
了铁磁介质磁导率随应力线性变化的理论公式, 其
中铁磁性构件在受到大小为 σ 的应力作用下产生的
为
应力能E σ
3
E σ =- σλ σ cosθ ( 7 )
2
2
为各向磁致伸
式中: θ 为应力与磁化方向的夹角; λ σ
缩系数。
其中, 文献[ 15 ] 推导得到了力磁函数关系
图3 拉伸试件结构示意
3
1
2023年 第45卷 第3期
无损检测