Page 70 - 无损检测2023年第一期

李昱函, 等:

基于 ERT 技术的混凝土渗透无损检测

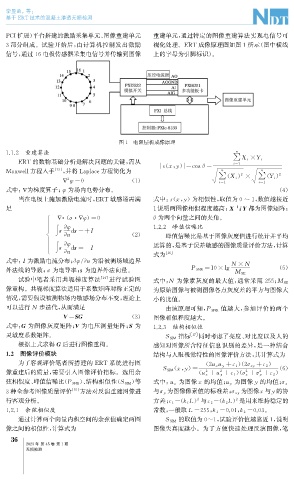
PCI 扩展) 平台搭建的激励采集单元、 图像重建单元 重建单元, 通过特定的图像重建算法实现电信号可
3部分组成。试验开始后, 由计算机控制发出激励 视化处理。 ERT 成像原理图如图1所示( 图中横线
信号, 通过16电极传感器采集电信号并传输到图像 上的字母为引脚标识)。

图1 电阻层析成像原理
1.1.2 重建算法 n
ERT 的数物基础分析是解决问题的关键, 需从 ∑ X i× Y i
i = 1
y =
Maxwell 方程入手 [ 13 ] , 并将 La p lace方程简化为 s ( x , ) cosθ= n n
2
2
∑ ( X i ) × ∑ ( Y i )
肀 2 φ= 0 ( 1 ) i = 1 i = 1
式中: 肀为梯度算子; 为场内电势分布。 ( 4 )
φ
当在电极上施加激励电流时, ERT 敏感场需满 式中: s ( x , ) 为相似性, 取值为0~1 , 数值越接近
y
足 1说明两图像相似程度越高; X 与 Y 都为图像矩阵;
φ =
肀 ·( σ ·肀 ) 0 θ 为两个向量之间的夹角。
∂ φ 1.2.2 峰值信噪比
σ ds=+ I

∫ ∂n ( 2 ) 峰值信噪比是基于图像灰度值进行统计并平均
∂ φ 运算的, 是基于误差敏感的图像质量评价方法, 计算
σ ds=- I

∫ ∂n 式为 [ 16 ]

式中: I 为激励电流分布; ∂ φ ∂ n 为沿被测场域边界
/
N ×N
外法线的导数; σ 为电导率; s 为边界外法向量。 P SNR= 10× l g ( 5 )
M SE
试验中笔者采用共轭梯度算法 [ 14 ] 进行试验图
式中: N 为像素灰度的最大值, 通常采用 255 ; M SE
像重构。共轭梯度算法适用于系数矩阵对称正定的 为原始图像与被测图像各点灰度差的平方与图像大
情况, 需要假设被测物场内敏感场分布不变, 理论上 小的比值。
可以进行 N 步迭代, 从而满足 值越大, 参加评价的两个
由该原理可知, P SNR
V= SG ( 3 ) 图像相似程度越大。
式中: G 为图像灰度矩阵; V 为电压测量矩阵; S 为 1.2.3 结构相似性
灵敏度系数矩阵。 指标 [ 17 ] 同时考虑了亮度、 对比度以及人的
S SIM
根据上式求得G 后进行图像重构。 感知对图像所含特征信息识别的差异, 是一种结合
1.2 图像评价模块 结构与人眼视觉特性的图像评价方法, 其计算式为
为了客观评价笔者所搭建的 ERT 系统进行图 ( 2 u x u y + c 1 2σ x y + c 2 )
)(
y =
(
像重建后的质量, 需要引入图像评价指标。选用余 S SIM x , ) ( u x + u y + c 1 σ x + σ y + c 2 ) ( 6 )
2
2
2
2
)(
) 等 为图像
弦相似度、 峰值信噪比( P SNR )、 结构相似性( S SIM 式中: u x 为图像 x 的均值; u y y 的均值; σ x
3种全参考图像质量评价 [ 15 ] 方法对反演重建图像进 与 σ y 为图像像素值的标准差; σ x y 为图像 x 与 的协
y
(
行客观分析。 方差; c 1=k 1 L )与 c 2=k 2 L )是用来维持稳定的
2
2
(
1.2.1 余弦相似度 常数, 一般取L= 255 , k 1= 0.01 , k 2= 0.03 。
通过计算两个向量内积空间的余弦值确定两图 的取值为0~1 , 试验评价值越靠近1 , 说明
S SIM
像之间的相似性, 计算式为 图像失真度越小。为了方便快速处理反演图像, 笔
6
3
2023年 第45卷 第1期
无损检测