Page 99 - 无损检测2022年第十期

冉毅川,等:
一种用于超声螺栓预紧力测量的时延算法

较低, 若不采用插值算法, 其预紧力分辨率不能满足 令 F = σ , 则螺栓应力测量公式可简化为
工程测量的分辨率需求。为进一步降低预紧力分辨 ) ( 8 )
F =K ( t σ - t 0
率, 常采用时域插值算法。但对于超声回波信号而 式中: F 为螺栓预紧力( 拉力为正, 压力为负); K 为
言, 时域插值算法存在计算量比较大的问题, 计算复 影响预紧力的系数。
杂, 无法满足实时测量的要求 [ 4 ] 。 式( 8 ) 表示弹性范围内螺栓预紧力与零应力状
基于此, 首先分析了超声螺栓预紧力测量原理, 态和加载应力状态下的渡越时间差成线性关系, 简
得到纵波法预紧力测量公式, 并搭建了超声螺栓预 化了超声波法对螺栓应力的测量。
紧力测量系统; 其次分别对频域升采样原理、 频域互 1.2 测量系统
相关时延估计算法进行了理论推导, 并将二者相结 超声螺栓预紧力测量系统包括发射接收信号
合提出了一种用于超声预紧力测量的频域补零互相 单元和数据采集单元。发射接收信号单元由多通
关时延估计算法( ZPCC ); 最后通过仿真和测量进行 道的超声发射接收板卡中的 FPGA ( 现场可编程逻
验证, 结果表明该方法能够精确快速地实现超声螺 辑门阵列) 控制模块控制, 高压发射模块和回波处
栓的预紧力测量, 且效果明显优于传统算法效果。 理模块完成信号的发射和接收。数据采集单元由

一块采样率达 1.25GHz的数据采集卡构成, 实现
1 超声螺栓预紧力测量方法
数据采集和模数转换功能。工控机协调控制发射
1.1 测量原理 接收信号 单 元 和 数 据 采 集 单 元, 并 对 超 声 信 号 进
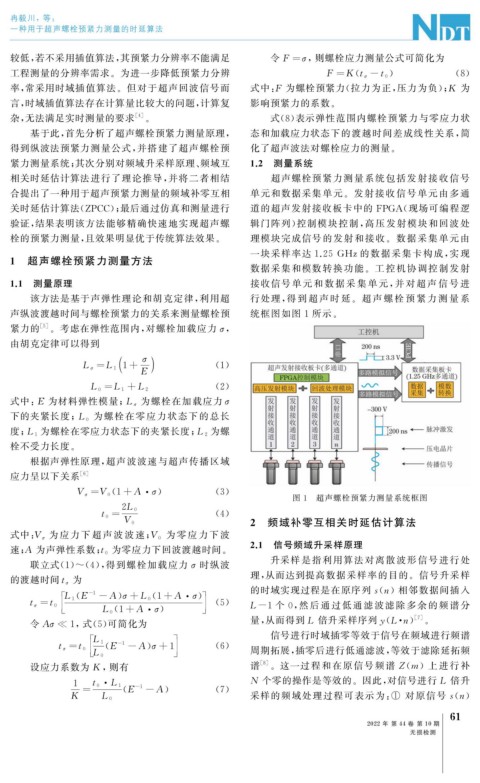
该方法是基于声弹性理论和胡克定律, 利用超 行处理, 得 到 超 声 时 延。超 声 螺 栓 预 紧 力 测 量 系
声纵波渡越时间与螺栓预紧力的关系来测量螺栓预 统框图如图 1 所示。
紧力的 [ 5 ] 。考虑在弹性范围内, 对螺栓加载应力σ ,
由胡克定律可以得到
σ

L σ =L 1 1+ E ( 1 )
( 2 )
L 0 =L 1 +L 2
为螺栓在加载应力σ
式中: E 为材料弹性模量; L σ
为螺栓在零应力状态下的总长
下的夹紧长度; L 0
为螺
度; L 1 为螺栓在零应力状态下的夹紧长度; L 2
栓不受力长度。
根据声弹性原理, 超声波波速与超声传播区域
应力呈以下关系 [ 6 ]
V σ = V 0 1+A· σ ) ( 3 )
(
图 1 超声螺栓预紧力测量系统框图
2L 0
t 0 = ( 4 )
2 频域补零互相关时延估计算法
V 0
为 零 应 力 下 波
式中: V σ 为 应 力 下 超 声 波 波 速; V 0
2.1 信号频域升采样原理
为零应力下回波渡越时间。
速; A 为声弹性系数; t 0
联立式( 1 ) ~ ( 4 ), 得到螺栓加载应力σ 时纵波 升采样是指利用算法对离散波形信号进行处
理, 从而达到提高数据采样率的目的。信号升采样
为
的渡越时间 t σ
的时域实现过程是在原序列s ( n )相邻数据间插入
(
(

L 1 E - 1 -A ) σ+L 0 1+A· σ )

t σ = t 0 L 0 1+A· σ ) ( 5 ) L-1 个 0 , 然 后 通 过 低 通 滤 波 滤 除 多 余 的 频 谱 分
(
[ 7 ]
(·
令 Aσ ≪1 , 式( 5 ) 可简化为 量, 从而得到 L 倍升采样序列 y L n ) 。
信号进行时域插零等效于信号在频域进行频谱
L 1
t σ = t 0 ( E - 1 -A ) σ+1 ( 6 ) 周期拓展, 插零后进行低通滤波, 等效于滤除延拓频

L 0
设应力系数为 K , 则有 谱 [ 8 ] 。这一过程和在原信号频谱 Z ( m )上 进 行 补
· N 个零的操作是等效的。因此, 对信号进行 L 倍升
1 t 0 L 1 ( E - 1 -A ) ( 7 )
=
K L 0 采样的频域处理过程可表示为: ① 对原信号s ( n )
1
6
2022 年 第 44 卷 第 10 期
无损检测