Page 102 - 无损检测2022年第十期
P. 102
冉毅川,等:
一种用于超声螺栓预紧力测量的时延算法
从表2可以看出, 针对该试验可选取螺栓应力系 5 倍, 这说明频域补零互相关算法在具备传统算法
数 K=1.680MPa · ns ; 同时可以看出 Pearson系数 测试精度的同时, 还拥有更快的运算速度。
-1
大于0.99 , 说明标定数据具有良好的线性关系。
3.2.2 螺栓预紧力测量 4 结语
为验证 ZPCC 算法的有效性, 在拉伸机上对螺 根据声弹性原理和胡克定律推导了纵波法预紧
栓以 20 MPa 为步长进行加载, 待加载载荷稳定后 力测量公式, 搭建了超声螺栓预紧力测量系统, 该系
采集超声回波信号, 并选取相同长度波形( 约10000 统最高硬件采样率可达 1.25GHz , 硬件声时分辨率
点), 使用 MATLAB 软件在 dell7910 工作站上利 为0.8ns ; 通过将频域升采样原理、 频域互相关时延
用线性插值互相关算法( LCC )、 三次插值互相关算 估计算法相结合, 提出了一种用于超声预紧力测量
法( PCC )、 三样条插值互相关算法( SCC ) 和频域补 的频域补零互相关时延估计算法; 采用仿真的方式
零互相关 算 法 插 值 16 倍 计 算 其 时 延 Δ t , 结 合 式 验证了互相关时延算法在低信噪比条件下, 具有一
( 8 ), 得到测量预紧力, 并与加载值进行对比, 利用式 定的降噪能力, 且计算结果稳定。
( 10 ) 计算相对误差值, 不同插值时延估计算法测试 选取 8.8 级 M30×150 碳 钢 螺 栓 进 行 标 定 试
结果如表 3 所示, 不同算法误差曲线如图 9 所示。 验, 确定了该型 号 螺 栓 的 应 力 系 数 为 1.680 MPa ·
ns ; 对该型号螺栓的加载试验结果表明, 频域补零
-1
σ test- σ ref
δ= ×100% ( 10 )
σ ref 互相关算法测试精度可达 3.5% , 与传统算法相当,
为超声法测量得到的轴向
式中: δ 为相对误差; σ test 但运算速度提升了 500% 。
为拉伸机加载的轴向应力。
应力; σ ref
参考文献:
[ 1 ] 李光, 莫亚梅, 吴努 . 螺栓轴向应力测量技术的研究概
况及展望 [ J ] . 南 通 大 学 学 报 ( 自 然 科 学 版), 2009 , 8
( 3 ): 67-71.
[ 2 ] 孙新亚, 胡锦东, 谢朝阳 . 钢结构工程中高强度螺栓轴
向应力的超声测量技术[ J ] . 科技风, 2019 ( 36 ): 93.
[ 3 ] 王寅观 . 声弹法及其应力测量的超声技术[ J ] . 新技术
新工艺, 1989 ( 4 ): 13-15.
[ 4 ] 盛广铭, 吴中川, 王甲峰 . 通信信号变采样率频域实现
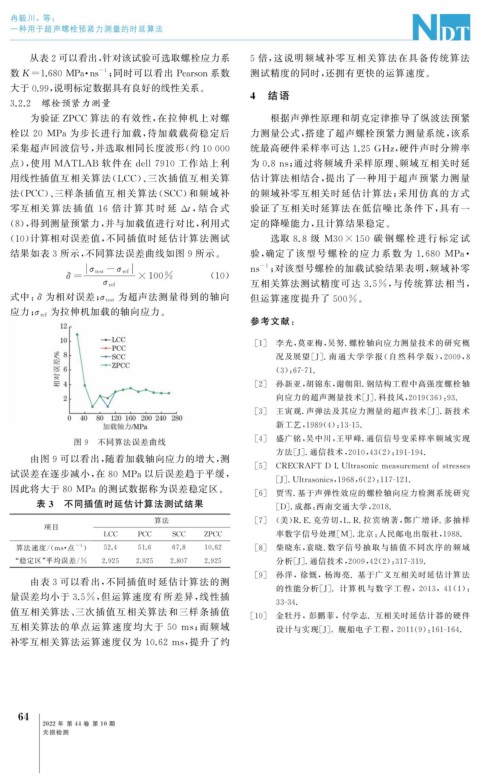
图 9 不同算法误差曲线
方法[ J ] . 通信技术, 2010 , 43 ( 2 ): 191-194.
由图 9 可以看出, 随着加载轴向应力的增大, 测
[ 5 ] CRECRAFTDI.Ultrasonicmeasurementofstresses
试误差在逐步减小, 在 80 MPa以后误差趋于平缓,
[ J ] .Ultrasonics , 1968 , 6 ( 2 ): 117-121.
因此将大于 80MPa的测试数据称为误差稳定区。
[ 6 ] 贾雪 . 基于声弹性效应的螺栓轴向应力检测系统研究
表 3 不同插值时延估计算法测试结果
[ D ] . 成都: 西南交通大学, 2018.
算法 [ 7 ] ( 美) R.E. 克劳切, L.R. 拉宾纳著, 鄷广增译 . 多抽样
项目
LCC PCC SCC ZPCC 率数字信号处理[ M ] . 北京: 人民邮电出版社, 1988.
算法速度 /( ms · 点 -1 ) 52.4 51.6 67.8 10.62 [ 8 ] 柴晓东, 袁晓 . 数字信号抽取与插值不同次序的频域
“ 稳定区” 平均误差 / % 2.925 2.925 2.807 2.925 分析[ J ] . 通信技术, 2009 , 42 ( 2 ): 317-319.
[ 9 ] 孙洋,徐慨,杨海亮 . 基于广义互相关时延估计算法
由表 3 可以看出, 不同插值时延估计算法的测
的性能分析[ J ] .计算机与数 字 工 程, 2013 , 41 ( 1 ):
量误差均小于 3.5% , 但运算速度有所差异, 线性插
33-34.
值互相关算法、 三次插值互相关算法和三样条插值 [ 10 ] 金牡丹,彭鹏菲,付学志 . 互相关时延估计器的硬件
互相关算法的单点运算速度均大于 50 ms ; 而频域 设计与实现[ J ] . 舰船电子工程, 2011 ( 9 ): 161-164.
补零互相关算法运算速度仅为 10.62ms , 提升了约
6
4
2022 年 第 44 卷 第 10 期
无损检测