Page 107 - 无损检测2021年第三期

胡家铖, 等:

一种改进的支持向量回归三轴管道漏磁缺陷量化方法

的谷谷间距、 峰峰间距、 峰谷间距、 拐点间距、 特殊点 d w X i X j
( , )
ex p -

间距、 峰谷差值、 体积、 表面积、 面能量等轴向、 径向 σ

, i ≠j
N
( , )
以及周向三轴信号共 53 个主要特征。其中特殊点 p i j = d w X i X j ( 3 )
∑ ex p - σ

的计算方法如式( 1 ) 所示。 j= 1 , j≠ i

0 , i= j

Y di _ left= Y v _ left+ α×D p v _ left ( 1 )
式中: 为 X i 选择 X j 的概率, σ 为核宽度参数。
p i j
Y di _ ri g ht= Y v _ ri g ht+ α×D p v _ ri g htt
针对整个分类的平均准确率 f ω ) 如式( 4 ) 所
(
, 为双边峰谷
式中: α 为特殊点系数; D p v _ left D p v _ ri g htt
, , 为双边 示, 其中 N 为样本的个数, 当正确分类, 即 y i = y j
差值; Y v _ left Y v _ ri g ht 为双边谷值; Y di _ left Y di _ ri g ht
时, =1 ; 当错误分类时 y i j =0 ; 特征选择目标函
特殊点值。 y i j
数 F ( ω ) 在 f ω ) 中加λ 正则化项, 如式( 5 ) 所示, 其
(
3 基于近邻成分分析的特征选择方法 中λ 为正则化参数。
1
在对实际问题进行研究的过程中, 为了能够全 f w ) = ∑∑ y i j p i j ( 4 )
(
N i j
面准确地反映出事物的特征和发展规律, 往往需要
d
尽可能多地考虑有关事物的多项数据指标, 避免遗 F ( w ) = f w ) λ ∑ w m ( 5 )
2
-
(
m=1
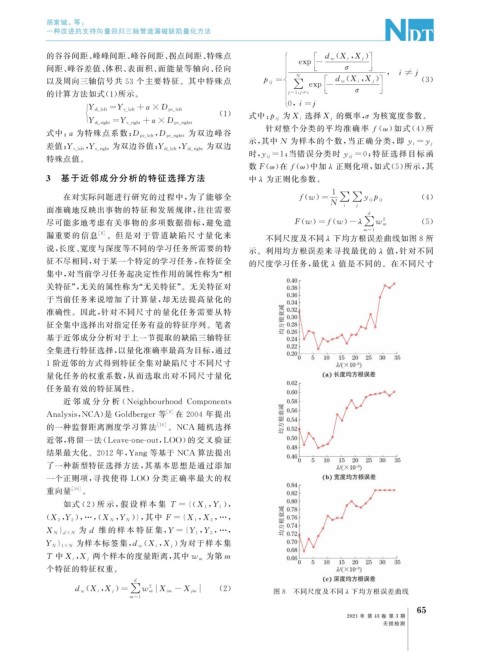
漏重要的信息 [ 6 ] 。但是对于管道缺陷尺寸量化 来 不同尺度及不同λ 下均方根误差曲线如图8 所
说, 长度、 宽度与深度等不同的学习任务所需要的特 示。利用均方根误差来寻找最优的λ 值, 针对不同
征不尽相同, 对于某一个特定的学习任务, 在特征全 的尺度学习任务, 最优λ 值是不同的。在不同尺寸
集中, 对当前学习任务起决定性作用的属性称为“ 相
关特征”, 无关的属性称为“ 无关特征”。无关特征对
于当前任务来说增加了计算量, 却无法提高量化的
准确性。因此, 针对不同尺寸的量化任务需要从特
征全集中选择出对指定任务有益的特征序列。笔者
基于近邻成分分析对于上一节提取的缺陷三轴特征
全集进行特征选择, 以量化准确率最高为目标, 通过
1 阶近邻的方式得到特征全集对缺陷尺寸不同尺寸
量化任务的权重系数, 从而选取出对不同尺寸量化
任务最有效的特征属性。

近 邻 成 分 分 析 ( Nei g hbourhood Com p onents
Anal y sis , NCA ) 是 Goldber g er等 [ 9 ] 在 2004 年提出
的一种监督距离测度学习算法 [ 10 ] 。 NCA 随机选择
近邻, 将留一 法 ( Leave-one-out , LOO ) 的交 叉验证
结果最大化。 2012 年, Yan g 等基于 NCA 算法提出
了一种新型特征选择方法, 其基本思想是通过添加
一个正则项, 寻找使得 LOO 分类正确率最大的权
重向量 [ 10 ] 。
, ),
如式 ( 2 ) 所 示, 假 设 样 本 集 T = {( X 1 Y 1
, , ,…,
, ),…,( X N Y N
( X 2 Y 2 )}, 其 中 F = { X 1 X 2
} , ,…,
X N d×N 为 d 维 的 样 本 特 征 集, Y = { Y 1 Y 2
} ( , ) 为对于样本集
Y N 1×N 为样本标签集, d w X i X j
, 为第 m
T 中 X i X j 两个样本的度量距离, 其中 w m
个特征的特征权重。
d
2
( , )
d w X i X j = ∑ w m X im -X j m ( 2 ) 图 8 不同尺度及不同λ 下均方根误差曲线
m=1
5
6

2021 年 第 43 卷 第 3 期
无损检测