Page 108 - 无损检测2021年第三期

胡家铖, 等:

一种改进的支持向量回归三轴管道漏磁缺陷量化方法

学习任务对应最优λ 处, 基于 NCA 算法给出的不 性越大 [ 4 ] 。径向基核函数的核函数系数r 与惩罚系
数 C 的选择是决定 SVR 回归精度的关键。在参数
寻优的方法中, 常见的方法有网格搜索法、 遗传算
法、 粒子群算法等。
剑桥大学的 YANG 于 2010 年提出的蝙蝠算法
( BA ) 是一种通过种群的随机性( 即通过模仿蝙蝠利
用回声来进行定位的行为) 来实现寻优的全局优化
算法, 可实现在求解空间的寻优搜索。笔者利用随
机变异改进经典的 BA 算法, 使其能够跳出局部最
优的限制, 有更好的全局寻优能力, 对 SVR 算法进
行参数寻优, RVBA-SVR ( 随机变异蝙蝠 - 支持向量

回归) 算法的流程如图 10 所示。

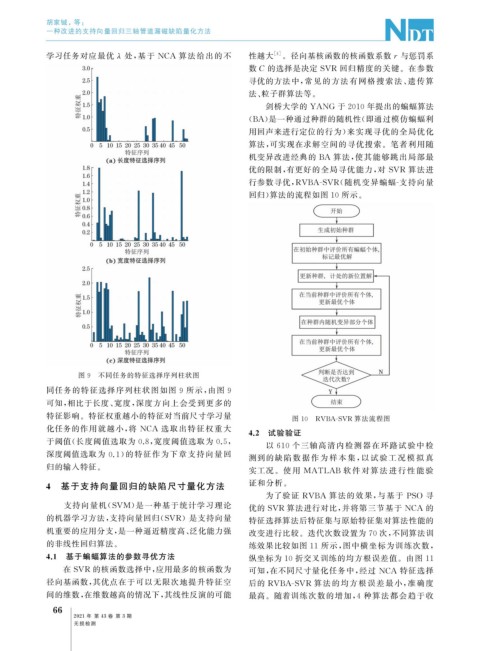
图 9 不同任务的特征选择序列柱状图
同任务的特征选择序列柱状图如图 9 所示, 由图 9
可知, 相比于长度、 宽度, 深度方向上会受到更多的
特征影响。特征权重越小的特征对当前尺寸学习量 图 10 RVBA-SVR 算法流程图
化任务的作用就越小, 将 NCA 选取出特征权重大
4.2 试验验证
于阈值( 长度阈值选取为 0.8 , 宽度阈值选取为 0.5 ,
以 610 个三轴高清内检测器在环路试验中检
深度阈值选取为 0.1 ) 的特征作为下章支持向量回
测到的缺 陷 数 据 作 为 样 本 集, 以 试 验 工 况 模 拟 真
归的输入特征。
实工况。使 用 MATLAB 软 件 对 算 法 进 行 性 能 验
4 基于支持向量回归的缺陷尺寸量化方法 证和分析。
为了验证 RVBA 算法的效果, 与基于 PSO 寻
支持向量机( SVM ) 是一种基于统计学习理论 优的 SVR 算法进行对比, 并将第三节基于 NCA 的

的机器学习方法, 支持向量回归( SVR )是支持向量 特征选择算法后特征集与原始特征集对算法性能的
机重要的应用分支, 是一种逼近精度高、 泛化能力强 改变进行比较。迭代次数设置为 70 次, 不同算法训
的非线性回归算法。 练效果比较如图 11 所示, 图中横坐标为训练次数,
4.1 基于蝙蝠算法的参数寻优方法 纵坐标为 10 折交叉训练的均方根误差值。由图 11
在 SVR 的核函数选择中, 应用最多的核函数为 可知, 在不同尺寸量化任务中, 经过 NCA 特征选择
径向基函数, 其优点在于可以无限次地提升特征空 后的 RVBA-SVR 算法的均方根误差最小, 准确度
间的维数, 在维数越高的情况下, 其线性反演的可能 最高。随着训练次数的增加, 4 种算法都会趋于收
6
6
2021 年 第 43 卷 第 3 期

无损检测