Page 67 - 无损检测2025年第二期
P. 67
孙尔雁,等:
CT 重建图像质量的优化算法
图 7 基于归一化频率的 Ramp 滤波器成像结果(增益系数 F A=5,频率取 1.5 次幂)
得更难以分辨。Ramp滤波器的不合理设计还可能 π
H ( )=F ω ω sin c ω (8)
会导致图像的自然质地被过度强调或扭曲,影响图 A 2
像的自然外观。
其中的窗函数定义为
3 基于 Shepp-Logan修正滤波器的成像质 sin( )
x
cx
sin ( )= (9)
量研究 x
由于Ramp滤波器并不能同时良好地处理高低 按sin c函数的定义,x=0其值为1[sin c(0)=1],
频信号,因此还需要在使用Ramp滤波后,进一步进 其作用是减少高频增益的幅度,在图像边缘锐化和
行低通滤波或平滑处理,来调整高频放大的程度, 可允许的噪声范围内,获得二者的平衡,同时相应地
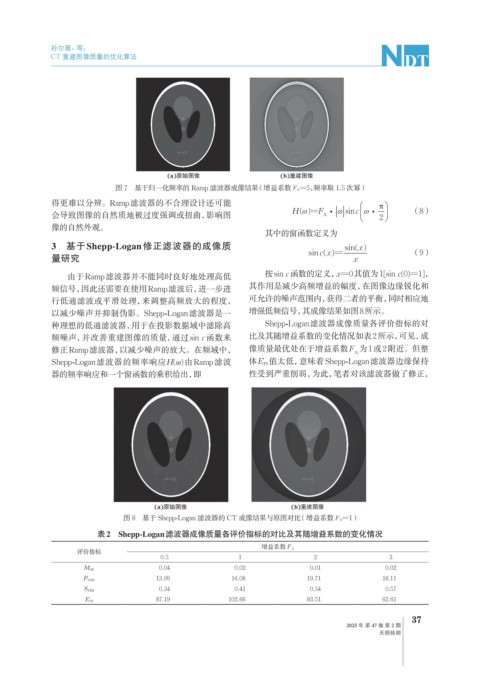
以减少噪声并抑制伪影。Shepp-Logan滤波器是一 增强低频信号,其成像结果如图8所示。
种理想的低通滤波器,用于在投影数据域中滤除高 Shepp-Logan滤波器成像质量各评价指标的对
频噪声,并改善重建图像的质量,通过sin c函数来 比及其随增益系数的变化情况如表2所示,可见,成
修正Ramp滤波器,以减少噪声的放大。在频域中, 像质量最优处在于增益系数F 为1或2附近。但整
A
Shepp-Logan滤波器的频率响应H(ω)由Ramp滤波 体E PI 值太低,意味着Shepp-Logan滤波器边缘保持
器的频率响应和一个窗函数的乘积给出,即 性受到严重削弱,为此,笔者对该滤波器做了修正,
图 8 基于 Shepp-Logan 滤波器的 CT 成像结果与原图对比(增益系数 F A=1)
表2 Shepp-Logan滤波器成像质量各评价指标的对比及其随增益系数的变化情况
评价指标 增益系数 F A
0.5 1 2 3
0.04 0.02 0.01 0.02
M SE
13.99 16.08 19.71 18.11
P SNR
0.34 0.41 0.54 0.57
S SIM
87.19 102.66 83.51 62.61
E PI
37
2025 年 第 47 卷 第 2 期
无损检测