Page 65 - 无损检测2025年第二期

孙尔雁，等：

CT 重建图像质量的优化算法

= AA =Wσ 1 π （5） 笔者对上述滤波反投影成像算法连续积分形式
τ
1 2 2 M proj 进行了离散近似，对滤波器和反投影步骤的数值实
由此可得投影数目与探测器像素之间的关系 现进行了程序设计和计算研究。标准Shepp-Logan
M proj ≈ π （6） phantom幻影灰度图（350×350）和正弦图如图2所
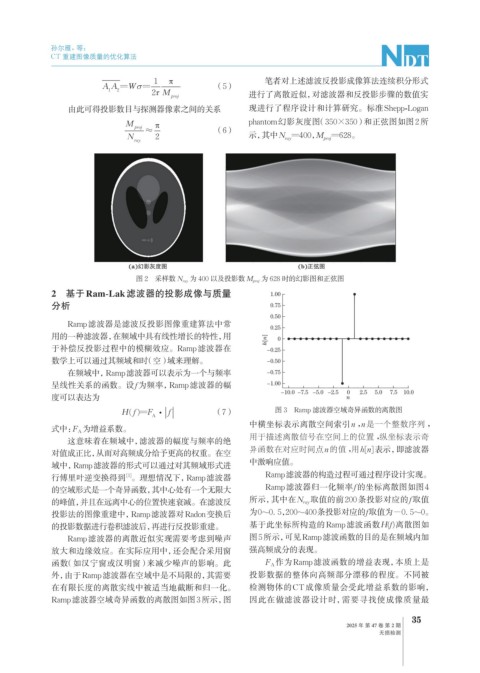
N ray 2 示，其中N =400，M =628。
ray
proj

图 2 采样数 N ray 为 400 以及投影数 M proj 为 628 时的幻影图和正弦图
2 基于Ram-Lak滤波器的投影成像与质量
分析

Ramp滤波器是滤波反投影图像重建算法中常
用的一种滤波器，在频域中具有线性增长的特性，用
于补偿反投影过程中的模糊效应。Ramp滤波器在
数学上可以通过其频域和时（空）域来理解。
在频域中，Ramp滤波器可以表示为一个与频率
呈线性关系的函数。设f为频率，Ramp滤波器的幅
度可以表达为
Hf f （7） 图 3 Ramp 滤波器空域奇异函数的离散图
( )=F

A
中横坐标表示离散空间索引n，n是一个整数序列，
式中： F A 为增益系数。
用于描述离散信号在空间上的位置， 纵坐标表示奇
这意味着在频域中，滤波器的幅度与频率的绝
异函数在对应时间点n的值， 用h[n]表示，即滤波器
对值成正比，从而对高频成分给予更高的权重。在空
中激响应值。
域中，Ramp滤波器的形式可以通过对其频域形式进
行傅里叶逆变换得到 。理想情况下，Ramp滤波器 Ramp滤波器的构造过程可通过程序设计实现。
[1]
的空域形式是一个奇异函数，其中心处有一个无限大 Ramp滤波器归一化频率f的坐标离散图如图4
的峰值，并且在远离中心的位置快速衰减。在滤波反 所示，其中在N ray 取值的前200条投影对应的f取值
为0~0. 5，200~400条投影对应的f取值为-0. 5~0。
投影法的图像重建中，Ramp滤波器对Radon变换后
的投影数据进行卷积滤波后，再进行反投影重建。 基于此坐标所构造的Ramp滤波函数H(f)离散图如
Ramp滤波器的离散近似实现需要考虑到噪声 图5所示，可见Ramp滤波函数的目的是在频域内加
放大和边缘效应。在实际应用中，还会配合采用窗 强高频成分的表现。
函数（如汉宁窗或汉明窗）来减少噪声的影响。此 F A 作为Ramp滤波函数的增益表现，本质上是
外，由于Ramp滤波器在空域中是不局限的，其需要 投影数据的整体向高频部分漂移的程度。不同被
在有限长度的离散实线中被适当地截断和归一化。 检测物体的CT成像质量会受此增益系数的影响，
Ramp滤波器空域奇异函数的离散图如图3所示，图 因此在做滤波器设计时，需要寻找使成像质量最

35
2025 年 第 47 卷 第 2 期
无损检测