Page 38 - 无损检测2024年第七期

王 堃，等：

基于机器视觉的火箭贮箱焊缝射线检测

入多输出的非线性系统，很难用精确模型描述，故传
统的控制方法不能满足伺服机构基于图像视觉的精
确运动要求。文章提出了一种基于SSA-BP的视觉
伺服自适应控制算法。
3.1 SSA-BP算法控制原理
BP神经网络在进行数据训练和迭代过程中，存
在易陷入局部最优、收敛速度慢，泛化能力差的缺
点。文章采用SSA麻雀搜索算法对BP神经网络的
初始权值与阈值进行优化，通过模拟麻雀觅食行为
和反捕食行为进行全局寻优，能有效避免BP神经网
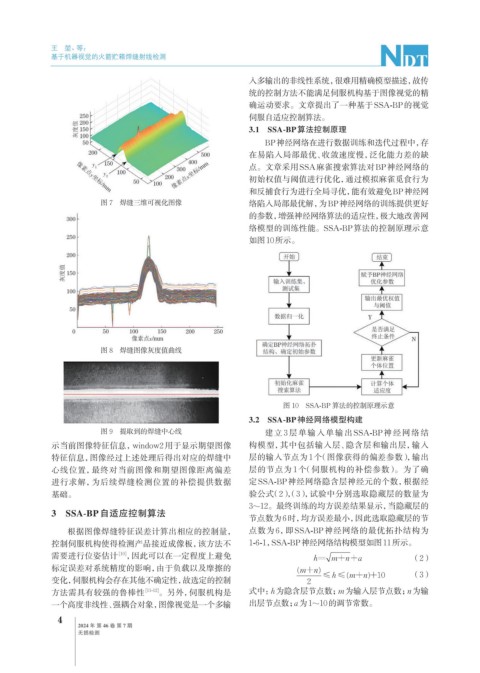
图 7 焊缝三维可视化图像 络陷入局部最优解，为BP神经网络的训练提供更好
的参数，增强神经网络算法的适应性，极大地改善网
络模型的训练性能。SSA-BP算法的控制原理示意
如图10所示。

图 8 焊缝图像灰度值曲线

图 10 SSA-BP 算法的控制原理示意
3.2 SSA-BP神经网络模型构建
图 9 提取到的焊缝中心线 建立 3 层单输入单输出SSA-BP神经网络结
示当前图像特征信息，window2用于显示期望图像 构模型，其中包括输入层、隐含层和输出层，输入
特征信息，图像经过上述处理后得出对应的焊缝中 层的输入节点为1个 （图像获得的偏差参数），输出
心线位置，最终对当前图像和期望图像距离偏差 层的节点为 1 个 （伺服机构的补偿参数）。为了确
进行求解，为后续焊缝检测位置的补偿提供数据 定SSA-BP神经网络隐含层神经元的个数，根据经
基础。 验公式（2），（3），试验中分别选取隐藏层的数量为
3~12。最终训练的均方误差结果显示，当隐藏层的
3 SSA-BP自适应控制算法
节点数为6时，均方误差最小，因此选取隐藏层的节
根据图像焊缝特征误差计算出相应的控制量， 点数为 6，即SSA-BP神经网络的最优拓扑结构为
控制伺服机构使得检测产品接近成像板，该方法不 1-6-1，SSA-BP神经网络结构模型如图11所示。
需要进行位姿估计 [10] ，因此可以在一定程度上避免 （2）
标定误差对系统精度的影响，由于负载以及摩擦的
（3）
变化，伺服机构会存在其他不确定性，故选定的控制
方法需具有较强的鲁棒性 [11-12] 。另外，伺服机构是 式中：h为隐含层节点数；m为输入层节点数；n为输
一个高度非线性、强耦合对象，图像视觉是一个多输 出层节点数；a为1~10的调节常数。
4
2024 年 第 46 卷 第 7 期
无损检测