Page 102 - 无损检测2023年第八期

薛 峰:
基于改进阈值函数的 TOFD 图像小波去噪

( 4 )文献[ 15 ] 所提的改进阈值函数 缘计算的集成, 从而在产品中进行实际应用, 文章中

(
ψ
s g n ( , )
f jk f j , k - 1- a ) 选取参数a 为0.8 。

f ( 7 )
' j , k = f j , k ≥ψ
3 改进阈值函数的小波去噪试验

0 f j , k <ψ

f 为去噪后的小波系数; , 为小波分解 3.1 改进阈值函数的小波去噪仿真
式中: ' j , k f jk
ψ=
系数; a 为改进阈值系数且0<a<1 ; 为阈值, 为了验证提出的小波阈值函数去噪的有效
ψ
性, 采用 MATLAB 软件对信号进行仿真试验, 小
σ 2lnN ( σ 为噪声信号的标准差, N 为信号长度);
波基函数选择db5小波函数, 分解层数为4层。阈
s g n ( , ) 为符号函数。
f jk
硬阈值函数在阈值 ψ 处不连续, 会造成重构信 值函数采用上一节列出的阈值函数和笔者提出的

号的震荡; 软阈值函数虽然为连续函数但有固定偏 改进小波阈值函数, 其中 =σ 2lnN 。 对上述5
ψ
差, 容易造成重构信号失真; 文献[ 14 ] 的改进阈值函 种小波阈值函数的去噪效果进行对比, 采用信噪
数虽然连续但是仍没有消除偏差; 文献[ 15 ] 的改进 比( S NR )、 均方根误差( R MSE ) 作为评价去噪效果的
阈值函数折中了软阈值函数与硬阈值函数, 但是对 指标, 即
于小于临界阈值的小波系数直接置零, 不能保留低 N
2
∑ x ( t )
能量信号。 i = 1

S NR= 10l g N ( 9 )
结合 TOFD检测的特性, 对小波分解后各个子 2
-

∑ [ x ( t ) 'x ( t )]

频带的小波系数的能量分布进行分析, 提出了一种改 i = 1
进的小波阈值函数, 该小波阈值函数在小波空间连续 1 N
2
R MSE= ∑ [ x ( t ) 'x ( t )] ( 10 )
-
且高阶可导, 同时能够有效克服软阈值函数产生的固 N i = 1
定偏差。笔者提出的改进阈值函数可表示为 式中: x ( t ) 为采集到的信号; 'x ( t ) 为去噪后的信号;
N 为采样点数。
a ψ

s g n ( , ) f j , k - f j , k - ψ+1 信号去噪后S NR 越大、 R MSE 越小表示越接近真
f jk
| f j , k|≥ψ 实信号。

f 利用小波工具箱加载leleccum 信号, 添加的噪
' j , k =
(
f j , k 1- a )
s g n ( , ) 声信号的信噪比为 25dB 。 MATLAB 软件生成的

f jk
ψ
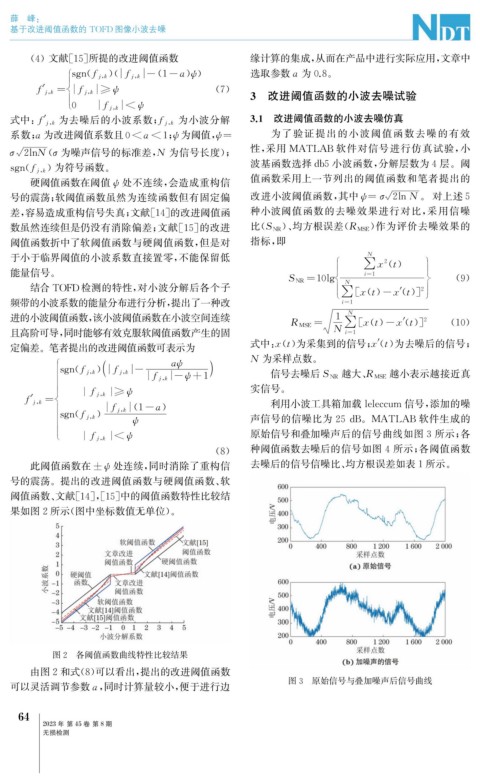
原始信号和叠加噪声后的信号曲线如图3所示; 各

| f j , k|<ψ

种阈值函数去噪后的信号如图4所示; 各阈值函数
( 8 )
此阈值函数在 ± ψ 处连续, 同时消除了重构信 去噪后的信号信噪比、 均方根误差如表1所示。
号的震荡。提出的改进阈值函数与硬阈值函数、 软
阈值函数、 文献[ 14 ],[ 15 ] 中的阈值函数特性比较结
果如图2所示( 图中坐标数值无单位)。
图2 各阈值函数曲线特性比较结果
由图2和式( 8 ) 可以看出, 提出的改进阈值函数
图3 原始信号与叠加噪声后信号曲线
可以灵活调节参数a , 同时计算量较小, 便于进行边

4
6
2023年 第45卷 第8期
无损检测