Page 57 - 无损检测2021年第八期
P. 57
余焕伟, 等:
基于高斯混合 - 隐马尔可夫模型的特种设备敲击检测
图 14 混入高斯白噪声前后的敲击声信号
声后的信噪比为30dB ( 假设原始信号中不含噪声),
此时模型 A 和 B 的识别率分别为 57.4% , 72.1% ; 在
信噪比为25dB 时, 则为 54.8% , 61.0% , 识别率随着
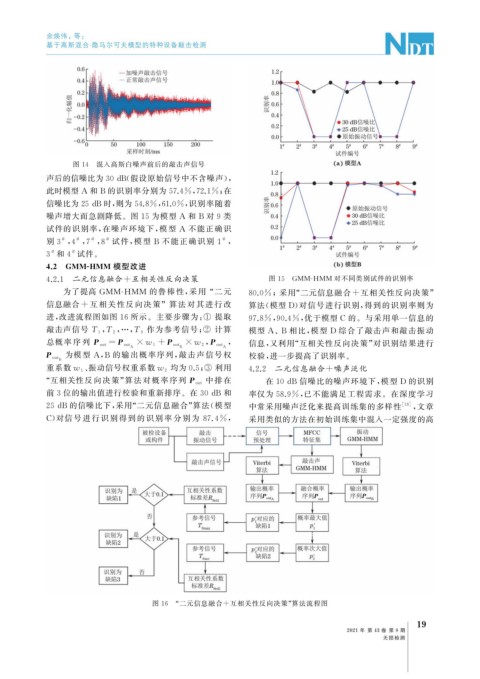
噪声增大而急剧降低。图 15 为模型 A 和 B 对 9 类
试件的识别率, 在噪声环境下, 模型 A 不能正确识
#
#
#
#
#
别 3 , 4 , 7 , 8 试件, 模型 B 不能正确识别 1 ,
#
#
3 和 4 试件。
4.2 GMM-HMM 模型改进
4.2.1 二元信息融合 + 互相关性反向决策 图 15 GMM-HMM 对不同类别试件的识别率
为了提高 GMM-HMM 的鲁棒性, 采用 “ 二元 80.0% ;采用“ 二元信息融合 + 互相关性反向决策”
信息融合 + 互相关性反向决策”算法 对 其 进 行 改 算法( 模型 D ) 对信号进行识别, 得到的识别率则为
进, 改进流程图如图 16 所示。主要步骤为: ① 提取 97.8% , 90.4% , 优于模型 C 的。与采用单一信息的
作为参考信号; ② 计算 模型 A 、 B 相比, 模型 D 综合了敲击声和敲击振动
, ,…, T 9
敲击声信号 T 1 T 2
, , 信息, 又利用“ 互相关性反向决策” 对识别结果进行
总概率 序 列 P out=P out ×w 1 +P out ×w 2 P out
A B A
为模型 A , B 的输出概率序列, 敲击声信号权
P out 校验, 进一步提高了识别率。
B
均为0.5 ; ③ 利用
重系数 w 1 、 振动信号权重系数 w 2 4.2.2 二元信息融合 + 噪声泛化
中排在 在 10dB 信噪比的噪声环境下, 模型 D 的识别
“ 互相关性反向决策” 算法对概率序列 P out
前 3 位的输出值进行校验和重新排序。在 30dB 和 率仅为 58.9% , 已不能满足工程需求。在深度学习
25dB 的信噪比下, 采用“ 二元信息融合” 算法( 模型 中常采用噪声泛化来提高训练集的多样性 [ 18 ] , 文章
C ) 对信 号 进 行 识 别 得 到 的 识 别 率 分 别 为 87.4% , 采用类似的方法在初始训练集中混入一定强度的高
图 16 “ 二元信息融合 + 互相关性反向决策” 算法流程图
9
1
2021 年 第 43 卷 第 8 期
无损检测