Page 46 - 无损检测2021年第三期
P. 46
唐 涛, 等:
基于相位测量轮廓术的车轮踏面三维轮廓测量
图 6 枝切法相位展开结果
图 7 改进枝切法相位展开结果
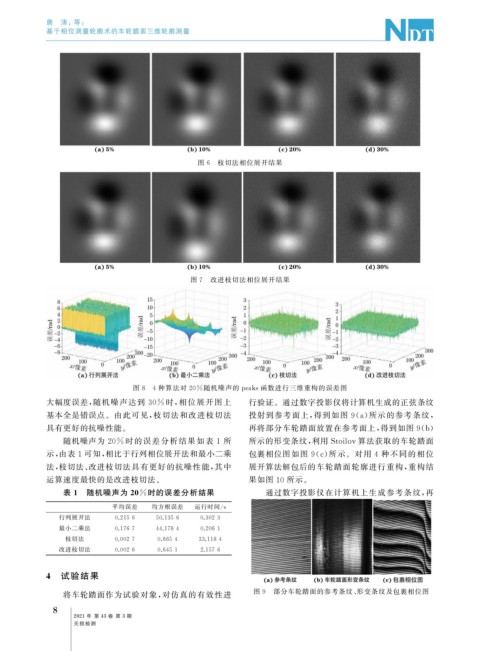
图 8 4 种算法对 20% 随机噪声的 p eaks函数进行三维重构的误差图
大幅度误差, 随机噪声达到 30% 时, 相位展开图上 行验证。通过数字投影仪将计算机生成的正弦条纹
基本全是错误点。由此可见, 枝切法和改进枝切法 投射到参考面上, 得到如图 9 ( a ) 所示的参考条纹,
具有更好的抗噪性能。 再将部分车轮踏面放置在参考面上, 得到如图 9 ( b )
随机噪声为 20% 时的误差分析结果如表 1 所 所示的形变条纹, 利用 Stoilov算法获取的车轮踏面
示, 由表 1 可知, 相比于行列相位展开法和最小二乘 包裹相位图如图 9 ( c ) 所示。对用 4 种不同的相位
法, 枝切法、 改进枝切法具有更好的抗噪性能, 其中 展开算法解包后的车轮踏面轮廓进行重构, 重构结
运算速度最快的是改进枝切法。 果如图 10 所示。
表 1 随机噪声为 20% 时的误差分析结果 通过数字投影仪在计算机上生成参考条纹, 再
平均误差 均方根误差 运行时间 / s
行列展开法 0.2156 50.1356 0.3023
最小二乘法 0.1767 44.1784 0.2061
枝切法 0.0027 0.6654 33.1184
改进枝切法 0.0026 0.6451 2.1576
4 试验结果
图 9 部分车轮踏面的参考条纹、 形变条纹及包裹相位图
将车轮踏面作为试验对象, 对仿真的有效性进
8
2021 年 第 43 卷 第 3 期
无损检测