Page 118 - 无损检测2024年第九期

程芳玲，等：
基于阈值和互相关的螺栓超声轴向应力测量算法

的重复性和实际可操作性，选取同样材料同样规格 测量，在施加较大轴向应力时，计算精度较高，稳定
#
#
的另外3根不同螺栓 （编号分别为1 ，2 ，3 ）分别施 性好。
#
加0，30，60，90，120，150，180 MPa轴向应力进行精 3.3 互相关算法
度验证，得到的结果如表2所示。 螺栓轴向应力测试环境存在设备振动、摩擦、碰
撞而产生的机械性噪声，为模拟现场工况环境采集
表2 螺栓轴力测量结果
到的超声信号，利用Matlab软件在上节的2 螺栓回
#
轴向预加载应力/ 测量结果/
螺栓编号 相对误差% 波信号中使用噪声函数，对信号分别叠加噪声信号
MPa MPa
0 −5.674 6 — 使得其信噪比分别为5，10，15，20，30，60 dB。叠加
30 32.149 4 7.164 7 噪声后信号如图12~图17所示。
60 58.901 9 1.830 1
1 # 90 89.479 6 0.578 2
120 122.588 3 2.156 9
150 153.665 9 2.443 9
180 181.910 2 1.061 2
0 −0.322 8 —
30 33.390 5 11.301 7
60 60.182 4 0.303 9
2 # 90 91.469 8 1.633 1
120 124.654 3 3.878 6
150 154.378 2 2.918 8
180 182.644 7 1.469 3
0 −11 —
30 22.310 4 25.632
图 12 5 dB 加噪延迟信号波形
60 46.336 2 22.773
3 # 90 91.774 3 1.971 4
120 122.673 5 2.227 9
150 148.691 0 0.872 7
180 179.155 1 0.469 4
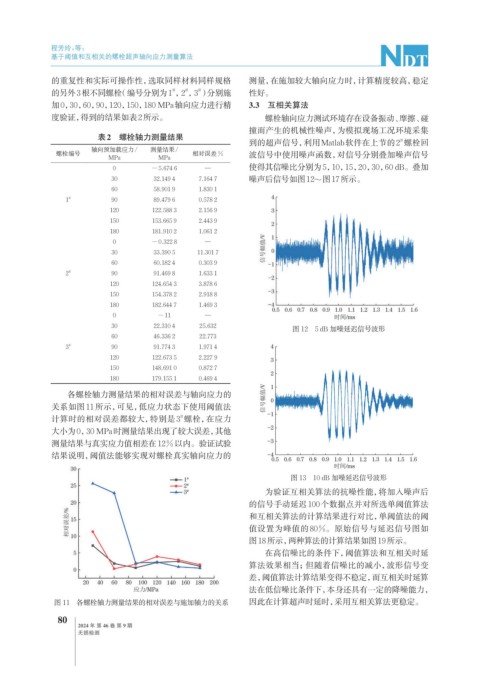
各螺栓轴力测量结果的相对误差与轴向应力的
关系如图11所示，可见，低应力状态下使用阈值法
计算时的相对误差都较大，特别是3 螺栓，在应力
#
大小为0，30 MPa时测量结果出现了较大误差，其他
测量结果与真实应力值相差在12%以内。验证试验
结果说明，阈值法能够实现对螺栓真实轴向应力的

图 13 10 dB 加噪延迟信号波形
为验证互相关算法的抗噪性能，将加入噪声后
的信号手动延迟100个数据点并对所选单阈值算法
和互相关算法的计算结果进行对比，单阈值法的阈
值设置为峰值的 80%。原始信号与延迟信号图如
图18所示， 两种算法的计算结果如图19所示。
在高信噪比的条件下，阈值算法和互相关时延
算法效果相当；但随着信噪比的减小，波形信号变
差，阈值算法计算结果变得不稳定，而互相关时延算
法在低信噪比条件下，本身还具有一定的降噪能力，

图 11 各螺栓轴力测量结果的相对误差与施加轴力的关系 因此在计算超声时延时，采用互相关算法更稳定。
80
2024 年 第 46 卷 第 9 期
无损检测