Page 114 - 无损检测2024年第九期

程芳玲，等：
基于阈值和互相关的螺栓超声轴向应力测量算法

声波的传播时间。相比阈值算法，互相关算法在计算 由式（3），（4）分别计算出螺栓轴力的大小。
中利用了回波信号的整体信息，因而具有较强的抗噪 使用横纵波法的前提条件是需要知道无应力状
能力和更高的计算精度与稳定性。然而，其缺陷在于 态下超声波在螺栓中传播的时间，引入两个新参数
无法直接求出超声横纵波法所需的初始渡越时间。 N 和N ，分别定义为
σ
0
基于此，文章设计了阈值互相关算法并进行了
（5）
阈值算法和互相关算法在超声波渡越时间测量中的
应用，以评估其在轨道列车螺栓预紧力测量中的适
由式（3），（4）可以推出
用性和精度，为提高轨道列车螺栓预紧力测量的准
（6）
确性和可靠性提供技术支持。
式中：N 只与材料本身有关，可以通过试验标定测
0
1 基本原理 得，也可以通过理论计算得到；t ,t 分别为零应力
T0
L0
t
1.1 螺栓轴向应力测量原理 状态下的横波传播时间和纵波传播时间； ,t 分别
Lσ
Tσ
为应力状态下螺栓横，纵波的传播时间。
假设螺栓只受到轴向应力作用，在这种应力状
对螺栓进行标定试验时，对于同一批次螺栓，仅
态下，螺栓内超声横、纵波沿螺栓轴向的传播速度可
需要对一颗螺栓做一次试验即可。在实际测量中，
以分别表示为 [2]
只需要分别测得横纵波在螺栓中传播的时间tTσ 和
V =V (1- 1 σ) （1） tLσ 就可以通过式（5）确定螺栓轴力，并且可以忽略
T T0
2 μ
螺栓长度由于拉应力而产生的变化，不需要测量螺
 U  栓长度。
V =V  1- σ  （2）
L L0   λ 2( μ+2 )   1.2 阈值算法基本原理
式中：V ，V 分别表示横、纵波的传播速度；λ，μ 分别 阈值法的基本原理是通过确定回波信号特征点
T
L
为二阶弹性常数，即Lame常数；下标0和σ 分别表 的时间来确定超声波的渡越时间值，再通过渡越时
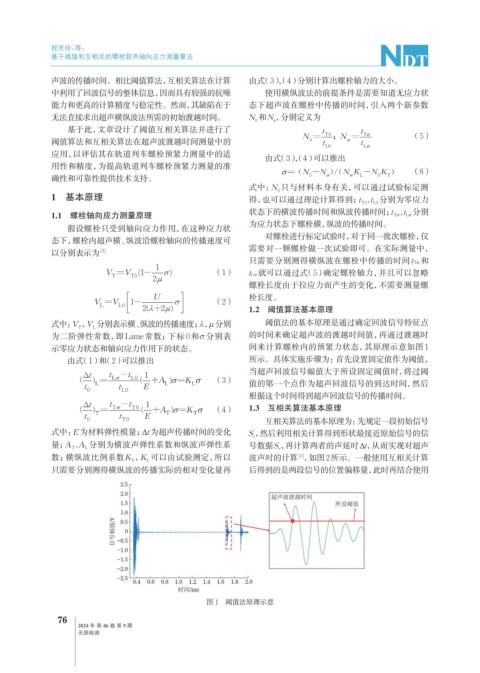
示零应力状态和轴向应力作用下的状态。 间来计算螺栓内的预紧力状态，其原理示意如图1
由式（1）和（2）可以推出 所示。具体实施步骤为：首先设置固定值作为阈值，
当超声回波信号幅值大于所设固定阈值时，将过阈
（3） 值的第一个点作为超声回波信号的到达时间，然后
根据这个时间得到超声回波信号的传播时间。

（4） 1.3 互相关算法基本原理
互相关算法的基本原理为：先规定一段初始信号
式中：E为材料弹性模量；Δt为超声传播时间的变化 S ，然后利用相关计算得到形状最接近原始信号的信
s
量；A ,A 分别为横波声弹性系数和纵波声弹性系 号数据S ，再计算两者的声延时Δt，从而实现对超声
r
T
L
数；横纵波比例系数K ，K 可以由试验测定，所以 波声时的计算 ，如图2所示。一般使用互相关计算
[3]
T L
只需要分别测得横纵波的传播实际的相对变化量再 后得到的是两段信号的位置偏移量，此时再结合使用

图 1 阈值法原理示意
76
2024 年 第 46 卷 第 9 期
无损检测