Page 72 - 无损检测2023年第四期

程树云, 等:

SSA 降噪算法在超声检测中的应用

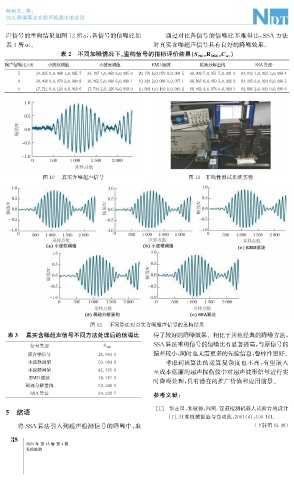
声信号的重构结果如图12所示, 各信号的信噪比如 通过对比各信号的信噪比不难得出, SSA 方法
表3所示。 对真实含噪超声信号具有良好的降噪效果。
, , )

表2 不同加噪情况下, 重构信号的指标评价结果( S NR R MSE C orr
小波软阈值 小波硬阈值 EMD滤波 稀疏分解重构 SSA算法
噪声信噪比 / dB

5 34.2050 , 0.0681 , 0.9857 34.1971 , 0.0696 , 0.9850 20.1706 , 0.0708 , 0.9845 69.9097 , 0.0517 , 0.9919 64.9431 , 0.0233 , 0.9984

0 30.4080 , 0.0792 , 0.9808 30.4625 , 0.0806 , 0.9801 19.3992 , 0.0883 , 0.9771 68.8656 , 0.0502 , 0.9922 64.3956 , 0.0246 , 0.9982

-5 17.7116 , 0.1254 , 0.9596 17.7342 , 0.1268 , 0.9589 15.8584 , 0.1502 , 0.9452 68.5624 , 0.0755 , 0.9843 64.8852 , 0.0430 , 0.9966

图10 真实含噪超声信号 图11 非线性测试系统实物

图12 不同算法对真实含噪超声信号的重构结果
表3 真实含噪超声信号不同方法处理后的信噪比 得了较好的降噪效果。相比于其他经典的降噪方法,

信号类型 S NR SSA 算法重构信号的信噪比有显著提高, 与原信号的

原含噪信号 25.9635 偏差较小, 同时也无需更多的先验信息, 鲁棒性更好。

小波软阈值 50.0848 考虑到该算法的运算复杂度也不高, 有望嵌入

小波硬阈值 41.7650 至成本低廉的超声探伤仪中对超声波形信号进行实

EMD滤波 38.7670
时降噪处理, 具有潜在的推广价值和应用前景。

稀疏分解重构 58.2485
SSA 算法 60.9287 参考文献:

[ 1 ] 华正汉, 朱敬德, 周明. 管道检测机器人试验台的设计
5 结语
[ J ] . 江苏机械制造与自动化, 2001 ( 4 ): 100-101.
将SSA 算法引入到超声检测信号的降噪中, 取 ( 下转第81页)
8
3
2023年 第45卷 第4期
无损检测