Page 55 - 无损检测2022年第七期
P. 55
贾昊天,等:
基于神经网络的表面波频散曲线反演温度相关杨氏模量
表 1 铝板温度场计算参数 1.2.1 神经网络模型的输入与输出
参数 公式( 或数值) 温度范围 /( ℃ ) 神经网络模型的输入数据应是易于获取, 且对
杨氏模量 /( GPa ) 70.857 ( 1-6.32e-4 T ) 0~400 材料杨氏模量的温度依赖性较高的。文章等距选取
剪切模量 /( GPa ) 26.99 ( 1-5.86e-4T ) 0~400 了 10~40MHz中的 31 个频率下的表面波速作为
密度 /( K g / m ) 2702-0.228 ( T-25 ) 0~Tm
3
神经网络的输入。神经网络的输出是材料杨氏模量
泊松比 /( 20 ℃ ) 0.31
温度分布函数的相关系数。由于在实际操作过程中
杨氏模量( 20 ℃ 下)/ GPa 69.96
热导率 /( W / m · K ) 226.23-0.085T 0~456 同时反演斜率k 和截距b 未取得较为理想的结果,
比热容 /( J / K g · K ) 913.57+0.488T 0~Tm 又因为常温( 20 ℃ ) 下的杨氏模量是已知的, 根据两
激光功率密度 /( W / m ) 2.8E8
2
点决定一条直线的原理, 反演 600 ℃ 材料杨氏模量
相对于常温下杨氏模量的比值, 就可以确定唯一的
杨氏模量与温度的线性关系。由于激活函数有效区
间的限制, 神经网络模型要求对输入数据进行标准
化处理, 所以将输入数据的每个维度映射为标准正
态分布。
1.2.2 训练样本
神经网络模型的训练样本由一系列的输入与输
出对组成。这些训练样本必须包含杨氏模量对温度
变化的所有可能。对 于 E ( T =600 ℃ ) =i% ×E
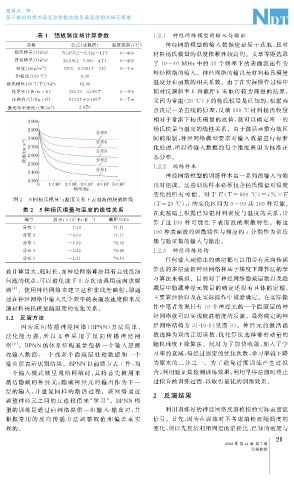
图 2 不同杨氏模量与温度关系下表面波的频散曲线
( T=20 ℃ ), i 的变化区间为 0~99 共 100 种可能。
表 2 5 种杨氏模量与温度的线性关系
在此基础上根据已知铝材料密度与温度的关系, 计
编号 斜率( ×10 Pa · K -1 ) 截距 / GPa
7
算了这 100 种可能性下表面波的频 散特性。将这
分布 1 -7.24 71.41
100种表面波的频散特性与相应的i 分别作为训练
分布 2 -6.03 71.17
集与验证集的输入与输出。
分布 3 -4.82 70.92
分布 4 -3.62 70.68 1.2.3 神经网络结构
分布 5 -2.41 70.44 任何输入到输出的映射都可以用带有反向传播
致计算量大、 耗时长, 而神经网络算法具有高效反演 算法的多层前馈神经网络和基于梯度下降算法的学
问题的优点, 可以避免成千上万次地调用前向求解 习算法来模拟。目前对于神经网络隐藏层数以及隐
器 [ 8 ] 。使用神经网络来建立这种非线性映射, 即通 藏层中隐藏神经元数量的确定还没有具体的定理,
过在神经网络中输入几个频率的表面波速度值来反 主要靠经验以及在实际操作中摸索确定。在实际操
演材料杨氏模量随温度的变化关系。 作中笔者发现具有 10 个神经元的一个隐藏层的神
1.2 反演方法 经网络就可以实现较高精度的反演。最终确定的神
经网络结构为 31-10-1 ( 见图 3 )。神经元的激活函
因 为 反 向 传 播 神 经 网 络 ( BPNN ) 方 法 简 单,
泛化 能 力 强, 所 以 文 章 采 用 了 反 向 传 播 神 经 网 数选择为双曲正切函数, 优化算法选择带有动量的
络 [ 9 ] 。 BPNN 的体系结构 通 常 包 括 一 个 输 入 层 接 随机梯度下降算法。同时为了加快收敛, 加入了学
收输入数 据, 一 个 或 多 个 隐 藏 层 处 理 数 据 和 一 个 习率的衰减, 每经过固定的优化次数, 学习率就下降
输出层表示识别结果。 BPNN 以前馈方式工作, 当 为原来的二分之一。为了避免过度训练产生过拟
一个输入 模 式 被 呈 现 给 网 络 时, 其 将 首 先 被 用 来 合, 利用验证集检测训练效果, 利用早停法随时终止
激活隐藏 的 神 经 元; 隐 藏 神 经 元 的 输 出 作 为 下 一 过拟合的训练过程, 以取得最优的训练效果。
层的输入, 并 重 复 同 样 的 激 活 过 程。 该 网 络 通 过 2 反演结果
调整神经元之间 的 互 连 权 值 来“ 学 习”。 BPNN 模
型的训练是通过向网络提 供 一 组 输 入 - 输 出 对, 并 利用训练好的神经网络反演模拟的实际表面波
根据常 用 的 反 向 传 播 方 法 调 整 权 值 和 偏 差 来 实 信号。首先, 因为在训练时不考虑泊松比随温度的
现的。 变化, 所以先反演利用固定的泊松比、 已知的密度与
1
2
2022 年 第 44 卷 第 7 期
无损检测