Page 38 - 无损检测2022年第五期
P. 38
郭 猛,等:
相控阵超声检测用喷水耦合喷嘴的优化设计
4 喷嘴的优化设计
4.1 道格拉斯 - 普克算法实现喷嘴的近似设计
文章设计的喷嘴存在一定的加工困难, 特别是
维多辛斯基曲线喷嘴在制造时, 要以维多辛斯基曲
线作为引导, 加工精度难以保证。因此在进行喷嘴
设计时, 需要采用一种近似方法, 对维多辛斯基曲线
喷嘴进行近似设计, 以达到在降低加工难度的同时,
保持较优的射流效果。
道格拉斯 - 普克算法是线状要素抽稀的经典算
法, 采用该算法可以保留曲线较大弯曲形态上的特
征点, 删除较小弯曲上的特征点, 有效地保持曲线的
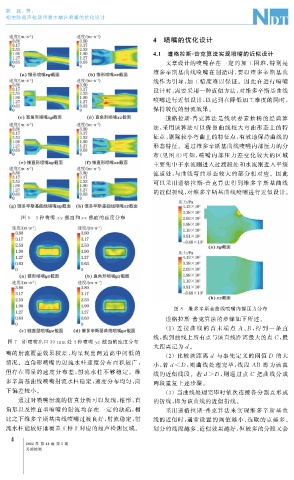
形态特征。通过维多辛斯基曲线喷嘴内部压力的分
布( 见图 8 ) 可知, 喷嘴内部压力差变化较大的区域
主要集中于水流刚进入过渡段处和水流刚进入平缓
流道处, 与曲线弯曲形态较大的部分相对应。因此
可以采用道格拉斯 - 普克算法得到维多辛斯基曲线
的近似折线, 对维多辛斯基曲线喷嘴进行近似设计。
图 6 4 种喷嘴 x y 截面和xz 截面的速度分布
图 8 维多辛斯基曲线喷嘴内部压力分布
道格拉斯 - 普克算法的步骤如下所述。
( 1 )连 接 曲 线 的 首 末 端 点 A 、 B , 得 到 一 条 直
线, 找到曲线上所有点与该直线距离最大的点 C , 最
图 7 距喷嘴出口 30mm 处 4 种喷嘴 y z 截面的速度分布
大距离记为d 。
嘴的射流覆盖效果较差, 均呈现出两边高中间低的 ( 2 )比较该距离 d 与事先定义的阈值 D 的大
情况。直角形喷嘴的射流水柱速度分布面积较广, 小, 若 d<D , 则曲线处理完毕, 线段 AB 即为该曲
但存在明显的速度分布差, 射流水柱不够稳定。维 线的近似线段。若d>D , 则通过点 C 把曲线分成
多辛斯基曲线喷嘴射流水柱稳定, 速度分布均匀, 向 两段重复上述步骤。
下偏差较小。 ( 3 )当曲线处理完毕时依次连接各分割点形成
通过对喷嘴射流的仿真分析可以发现, 锥形、 直 的折线, 即为该曲线的近似折线。
角形以及锥直型喷嘴的射流均存在一定的缺陷, 相 采用道格拉斯 - 普克算法来实现维多辛斯基曲
比之下维多辛斯基曲线喷嘴过渡良好, 射流稳定, 射 线的近似时, 通常设置的阈值越小、 选取的点越多、
流水柱能较好地覆盖工件上对应的超声检测区域。 划分的线段越多、 近似效果越好, 但较多的分段又会
4
2022 年 第 44 卷 第 5 期
无损检测