Page 45 - 无损检测2021年第十期
P. 45
张鑫明, 等:
奥氏体不锈钢应力腐蚀微裂纹的非线性表面波检测
需要较大的电脑内存和过长的运算时间。为使求 有属性, 主要与材料固有的物理特性有关。接触声
解过程准确, 时间步长必须满足奈奎斯特定理和 非线性反映了材料局部的缺陷特征, 其主要来源于
Moser 定理 [ 9 ] 。 界面、 裂纹缺陷、 接触面的非线性应力 - 应变等, 检测
奈奎斯特频率是指允许的最低抽样率, 即采样 过程中超声波振动使微裂纹界面发生周期性的张开
频率应不小于实际信号频率的2倍 [ 10 ] , 则时间步长 或闭合, 两个接触面相互撞击和摩擦, 这种裂纹张开
-8
t 1≤10×10 s 。 或闭合的状态导致其界面间存在各种应力 - 应变关
Moser定理是指一个周期的时间内至少包含 系, 其叠加会使得超声波信号产生非线性失真 [ 13 ] ,
-8
20个时间步, 则时间步长 t 2≤2×10 s 。 出现高次谐波。笔者所研究的非线性超声检测应力
综合考虑, 设置瞬态求解器的时间步长为 2× 腐蚀微裂纹问题则属于接触声非线性范畴。因此,
10 s , 求解的总时间应大于表面波传播至接收点 在创建微裂纹损伤的非线性表面波检测模型时不能
-8
-5
的时间, 设置为2×10 s 。 忽略微裂纹的接触声非线性, 需将微裂纹的两条边
1.5 边界条件 界定义为接触对( 分别为源边界与目标边界), 以确
1.5.1 低反射边界 保创建的非线性超声波检测微裂纹模型更合理, 较
由于模型的计算域尺寸很小, 当表面波传播至 好地实现非线性表面波对微裂纹的检测识别。
模型的边界时, 会发生很强的反射, 反射波与激励信 1.6 应力场与超声场的耦合
号产生混叠, 对接收信号产生干扰。因此, 为了降低 实际情况下, 无论是应力腐蚀还是疲劳腐蚀, 都
模型边界反射信号的干扰, 在模型边界处设置低反 是处于受力状态下的腐蚀损伤。在利用非线性表面
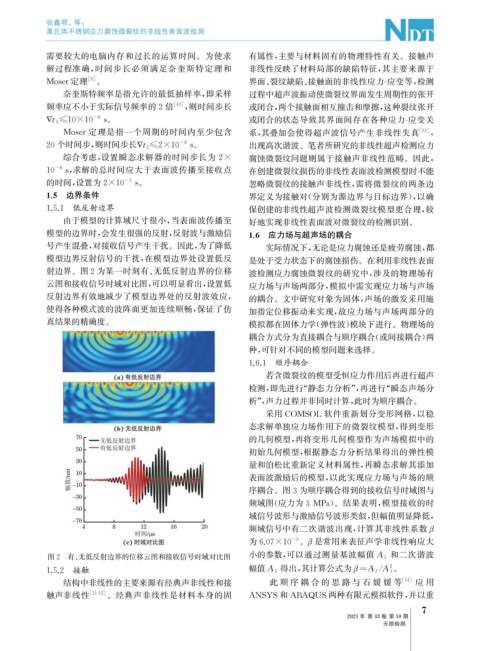
射边界。图2为某一时刻有、 无低反射边界的位移 波检测应力腐蚀微裂纹的研究中, 涉及的物理场有
云图和接收信号时域对比图, 可以明显看出, 设置低 应力场与声场两部分, 模拟中需实现应力场与声场
反射边界有效地减少了模型边界处的反射波效应, 的耦合。文中研究对象为固体, 声场的激发采用施
使得各种模式波的波阵面更加连续顺畅, 保证了仿 加指定位移振动来实现, 故应力场与声场两部分的
真结果的精确度。 模拟都在固体力学( 弹性波) 模块下进行。物理场的
耦合方式分为直接耦合与顺序耦合( 或间接耦合) 两
种, 可针对不同的模型问题来选择。
1.6.1 顺序耦合
若含微裂纹的模型受恒应力作用后再进行超声
检测, 即先进行“ 静态力分析”, 再进行“ 瞬态声场分
析”, 声力过程并非同时计算, 此时为顺序耦合。
采用 COMSOL 软件重新划分变形网格, 以稳
态求解单独应力场作用下的微裂纹模型, 得到变形
的几何模型, 再将变形几何模型作为声场模拟中的
初始几何模型, 根据静态力分析结果得出的弹性模
量和泊松比重新定义材料属性, 再瞬态求解其添加
表面波激励后的模型, 以此实现应力场与声场的顺
序耦合。图3为顺序耦合得到的接收信号时域图与
频域图( 应力为3MPa )。结果表明, 模型接收的时
域信号波形与激励信号波形类似, 但幅值明显降低,
频域信号中有二次谐波出现, 计算其非线性系数 β
为6.07×10 。 是常用来表征声学非线性响应大
-3
β
图2 有、 无低反射边界的位移云图和接收信号时域对比图 小的参数, 可以通过测量基波幅值 A 1 和二次谐波
2
1.5.2 接触 幅值 A 2 得出, 其计算公式为 =A 2 A 1 。
/
β
结构中非线性的主要来源有经典声非线性和接 此 顺 序 耦 合 的 思 路 与 石 媛 媛 等 [ 14 ] 应 用
触声非线性 [ 11-12 ] 。经典声非线性是材料本身的固 ANSYS和 ABAQUS两种有限元模拟软件, 并以重
7
2021年 第43卷 第10期
无损检测