Page 47 - 无损检测2021年第十期

张鑫明, 等:

奥氏体不锈钢应力腐蚀微裂纹的非线性表面波检测

2.1 恒应力作用下微裂纹深度对非线性表面波传
播行为的影响
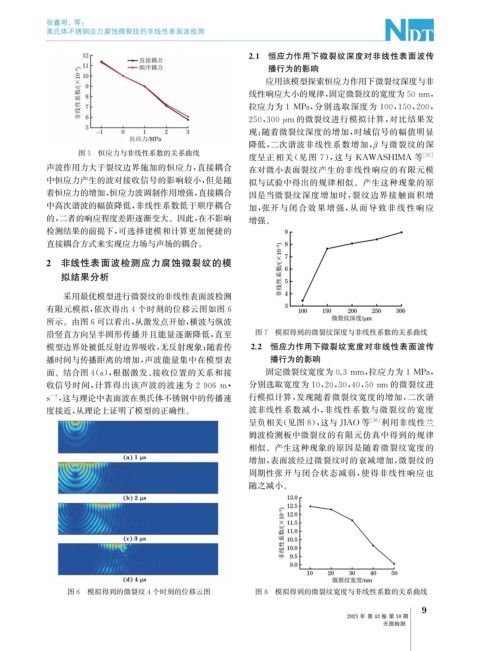
应用该模型探索恒应力作用下微裂纹深度与非

线性响应大小的规律, 固定微裂纹的宽度为50nm ,

拉应力为1 MPa , 分别选取深度为 100 , 150 , 200 ,

250 , 300 μ m 的微裂纹进行模拟计算, 对比结果发
现: 随着微裂纹深度的增加, 时域信号的幅值明显
降低, 二次谐波非线性系数增加, 与微裂纹的深
β
图5 恒应力与非线性系数的关系曲线
度呈正相关( 见图 7 ), 这与 KAWASHIMA 等 [ 15 ]
声波作用力大于裂纹边界施加的恒应力, 直接耦合 在对微小表面裂纹产生的非线性响应的有限元模
中恒应力产生的波对接收信号的影响较小, 但是随 拟与试验中得出的规律相似。产生这种现象的原
着恒应力的增加, 恒应力波调制作用增强, 直接耦合 因是当微裂纹深度增加时, 裂纹边界接触面积增
中高次谐波的幅值降低, 非线性系数低于顺序耦合 加, 张开与闭合效果增强, 从而导致非线性响应
的, 二者的响应程度差距逐渐变大。因此, 在不影响 增强。
检测结果的前提下, 可选择建模和计算更加便捷的

直接耦合方式来实现应力场与声场的耦合。
2 非线性表面波检测应力腐蚀微裂纹的模
拟结果分析

采用最优模型进行微裂纹的非线性表面波检测

有限元模拟, 依次得出4个时刻的位移云图如图6
所示。由图6可以看出, 从激发点开始, 横波与纵波
沿竖直方向呈半圆形传播并且能量逐渐降低, 直至 图7 模拟得到的微裂纹深度与非线性系数的关系曲线
模型边界处被低反射边界吸收, 无反射现象; 随着传 2.2 恒应力作用下微裂纹宽度对非线性表面波传
播时间与传播距离的增加, 声波能量集中在模型表 播行为的影响

面。结合图4 ( a ), 根据激发、 接收位置的关系和接 固定微裂纹宽度为0.3mm , 拉应力为1MPa ,

收信号时间, 计算得出该声波的波速为 2906m · 分别选取宽度为10 , 20 , 30 , 40 , 50nm 的微裂纹进
s , 这与理论中表面波在奥氏体不锈钢中的传播速 行模拟计算, 发现随着微裂纹宽度的增加, 二次谐
-1
度接近, 从理论上证明了模型的正确性。 波非线性系数减小, 非线性系数与微裂纹的宽度
呈负相关( 见图8 ), 这与JIAO 等 [ 16 ] 利用非线性兰
姆波检测板中微裂纹的有限元仿真中得到的规律
相似。产生这种现象的原因是随着微裂纹宽度的
增加, 表面波经过微裂纹时的衰减增加, 微裂纹的
周期性张开与闭合状态减弱, 使得非线性响应也
随之减小。

图6 模拟得到的微裂纹4个时刻的位移云图 图8 模拟得到的微裂纹宽度与非线性系数的关系曲线

9
2021年 第43卷 第10期
无损检测