Page 74 - 无损检测2021年第五期

褚英杰, 等:

17-4PH 不锈钢热老化的磁多参数无损评估

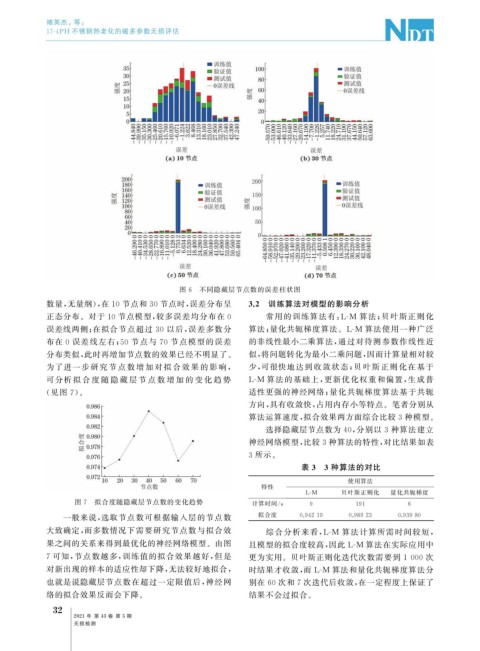
图 6 不同隐藏层节点数的误差柱状图
数量, 无量纲), 在 10 节点和 30 节点时, 误差分布呈 3.2 训练算法对模型的影响分析
常用的训练算法有: L-M 算法; 贝叶斯正则化
正态分布。对于 10 节点模型, 较多误差均分布在 0
误差线两侧; 在拟合节点超过 30 以后, 误差多数分 算法; 量化共轭梯度算法。 L-M 算法使用一种广泛
布在 0 误差线左右; 50 节点与 70 节点模型的误差 的非线性最小二乘算法, 通过对待测参数作线性近

分布类似, 此时再增加节点数的效果已经不明显了。 似, 将问题转化为最小二乘问题, 因而计算量相对较
为了进一 步 研 究 节 点 数 增 加 对 拟 合 效 果 的 影 响, 少, 可很快地达到收敛状态; 贝叶斯正则化在基于
可分析 拟 合 度 随 隐 藏 层 节 点 数 增 加 的 变 化 趋 势 L-M 算法的基础上, 更新优化权重和偏置, 生成普

( 见图 7 )。 适性更强的神经网络; 量化共轭梯度算法基于共轭
方向, 具有收敛快, 占用内存小等特点。笔者分别从
算法运算速度, 拟合效果两方面综合比较 3 种模型。
选择隐藏层节点数为 40 , 分别以 3 种算法建立
神经网络模型, 比较 3 种算法的特性, 对比结果如表
3 所示。
表 3 3 种算法的对比
使用算法
特性
L-M 贝叶斯正则化 量化共轭梯度
图 7 拟合度随隐藏层节点数的变化趋势
计算时间 / s 9 191 6

一般来说, 选取节点数可根据输入层的节点数 拟合度 0.94219 0.98923 0.93980
大致确定, 而多数情况下需要研究节点数与拟合效 综合分析来看, L-M 算法计算所需时间较短,
果之间的关系来得到最优化的神经网络模型。由图 且模型的拟合度较高, 因此 L-M 算法在实际应用中
7 可知, 节点数越多, 训练值的拟合效果越好, 但是 更为实用。贝叶斯正则化迭代次数需要到 1000 次

对新出现的样本的适应性却下降, 无法较好地拟合, 时结果才收敛, 而 L-M 算法和量化共轭梯度算法分
也就是说隐藏层节点数在超过一定限值后, 神经网 别在 60 次和 7 次迭代后收敛, 在一定程度上保证了
络的拟合效果反而会下降。 结果不会过拟合。
2
3

2021 年 第 43 卷 第 5 期
无损检测