Page 94 - 无损检测2025年第四期

王 硕，等：

基于集成算法的混凝土中钢筋直径涡流检测

)
式中： ( ，Kx x 为特征变量x 和x之间的核函数值； 量为n 和最大深度d 。
t
i i max
γ 为控制核函数宽度的超参数，防止模型在局部最优 （2）步骤2：随机抽取样本。从训练数据集D中
的情况下过拟合。 采用Bootstrap抽样法有放矢地随机抽取n个样本子集
（5）元学习器的选择 ，以创建每棵决策树的训练集。
随机森林（RF） 是由L.BREIMAN等提出的一 （3）步骤3：随机选择特征。在每个节点分裂时，
[23]
种将Bagging集成方法与随机子空间方法结合在一 随机选择特征。
起的机器学习算法。其通过构建多个决策树，再对 （4）步骤4：分裂节点。训练数据集中包含m个
它们的预测结果进行投票或者取平均值来得到最终 特征，则在每个节点随机选择 m 个特征进行分裂，
的回归结果。 直到达 到最大深度d 。重复步骤3、4，构建多棵决
max
随机森林可以很好地整合多个基学习器的预测 策树，直到达到预设的树的数量n 。
t
结果，有效融合SVM的预测结果，从而进一步提升 （5）步骤5：回归预测。在预测时采用取平均值
模型的泛化能力和预测准确性，具体实施步骤如下。 的方法对多棵决策树的预测结果进行汇总。
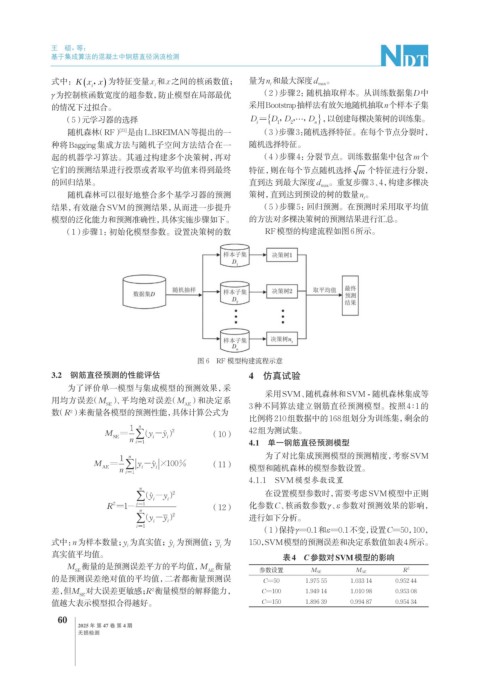
（1）步骤1：初始化模型参数。设置决策树的数 RF模型的构建流程如图6所示。

图 6 RF 模型构建流程示意
3.2 钢筋直径预测的性能评估 4 仿真试验
为了评价单一模型与集成模型的预测效果，采
采用SVM、随机森林和SVM - 随机森林集成等
用均方误差（M ）、平均绝对误差（M ）和决定系
SE AE 3种不同算法建立钢筋直径预测模型。按照4∶1的
数（R ）来衡量各模型的预测性能，具体计算公式为
2
比例将210组数据中的168组划分为训练集，剩余的
42组为测试集。
（10）
4.1 单一钢筋直径预测模型
为了对比集成预测模型的预测精度，考察SVM
（11） 模型和随机森林的模型参数设置。
4.1.1 SVM模型参数设置
在设置模型参数时，需要考虑SVM模型中正则
（12） 化参数C、核函数参数γ、ε 参数对预测效果的影响，
进行如下分析。
（1）保持γ=0.1和ε=0.1不变，设置C=50，100，
式中：n为样本数量；y 为真实值； 为预测值； 为 150，SVM模型的预测误差和决定系数值如表4所示。
i
真实值平均值。 表4 C参数对SVM模型的影响
M 衡量的是预测误差平方的平均值，M 衡量
SE AE 参数设置 M SE M AE R 2
的是预测误差绝对值的平均值，二者都衡量预测误 C=50 1.975 55 1.033 14 0.952 44
差，但M 对大误差更敏感；R 衡量模型的解释能力， C=100 1.949 14 1.010 98 0.953 08
2
SE
值越大表示模型拟合得越好。 C=150 1.896 39 0.994 87 0.954 34
60
2025 年 第 47 卷 第 4 期
无损检测