Page 90 - 无损检测2025年第一期

王婷婷，等：

基于改进 EFD- 小波去噪算法的岩石压裂声发射信号分类

基于树状滤波器组的谱峭度算法对信号的频 声会对频谱分割造成影响。改进后 EFD 算法能显
谱进行分割的结果如图 4 所示，可见，其能够利用 著体现有效信号与噪声信号的不同，具有更好的
峭度值对声发射信号所在频段进行定位。传统的 频谱分割性能。改进后 EFD 算法得到的各 FIBF
EFD 算法中 N 的不同选择会影响信号分解后的成 分量如图 5 所示，可见其能根据信号的特点和频率
分数量，在分解非平稳信号且背景噪声较大时，噪 进行分解。
0.1
1
幅值/V -1 0 幅值/V -0.5 0
0.5
0 100 200 300 400 500 600 700 800 900 1 000 0 100 200 300 400 500 600 700 800 900 1 000
采样点 采样点
(a) FIBF 1 (b) FIBF 2
1 0.5
幅值/V 0 幅值/V 0
-1
0 100 200 300 400 500 600 700 800 900 1 000 -0.5 0 100 200 300 400 500 600 700 800 900 1 000
采样点 采样点
(c) FIBF 3 0.2 (d) FIBF 4
0.1
幅值/V -0.1 0 幅值/V -0.2 0

0 100 200 300 400 500 600 700 800 900 1 000 0 100 200 300 400 500 600 700 800 900 1 000
采样点 采样点
(e) FIBF 5 (f) FIBF 6
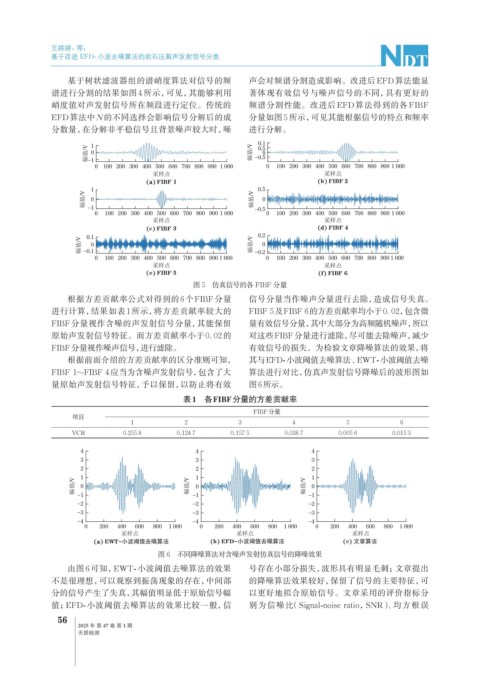
图 5 仿真信号的各 FIBF 分量
根据方差贡献率公式对得到的6 个FIBF分量 信号分量当作噪声分量进行去除，造成信号失真。
进行计算，结果如表 1 所示，将方差贡献率较大的 FIBF 5及FIBF 6的方差贡献率均小于0. 02，包含微
FIBF分量视作含噪的声发射信号分量，其能保留 量有效信号分量，其中大部分为高频随机噪声，所以
原始声发射信号特征。而方差贡献率小于0. 02的 对这些FIBF分量进行滤除，尽可能去除噪声，减少
FIBF分量视作噪声信号， 进行滤除。 有效信号的损失。为检验文章降噪算法的效果，将
根据前面介绍的方差贡献率的区分准则可知， 其与EFD-小波阈值去噪算法、EWT-小波阈值去噪
FIBF 1~FIBF 4应当为含噪声发射信号，包含了大 算法进行对比，仿真声发射信号降噪后的波形图如
量原始声发射信号特征，予以保留，以防止将有效 图6所示。
表1 各FIBF分量的方差贡献率
FIBF分量
项目
1 2 3 4 5 6
VCR 0.255 8 0.124 7 0.157 5 0.038 7 0.005 6 0.015 5

4 4 4
3 3 3
2 2 2
1 1 1
幅值/V 0 幅值/V 0 幅值/V 0
-1 -1 -1
-2 -2 -2
-3 -3 -3
-4 -4 -4
0 200 400 600 800 1 000 0 200 400 600 800 1 000 0 200 400 600 800 1 000
采样点 采样点 采样点
(a) EWT-小波阈值去噪算法 (b) EFD-小波阈值去噪算法 (c) 文章算法
图 6 不同降噪算法对含噪声发射仿真信号的降噪效果
由图 6 可知，EWT- 小波阈值去噪算法的效果 号存在小部分损失，波形具有明显毛刺；文章提出
不是很理想，可以观察到振荡现象的存在，中间部 的降噪算法效果较好，保留了信号的主要特征，可
分的信号产生了失真，其幅值明显低于原始信号幅 以更好地拟合原始信号。文章采用的评价指标分
值；EFD- 小波阈值去噪算法的效果比较一般，信 别为信噪比（Signal-noise ratio，SNR）、均方根误
56
2025 年 第 47 卷 第 1 期
无损检测