Page 95 - 无损检测2025年第一期

徐海丰，等：

基于 PSO 算法的储罐底板声发射源定位方法

效率。粒子群优化（PSO）算法因其强大的全局搜 粒子群中的每个成员会跟踪其到目前为止找到
索能力和较快的收敛速度，在提升定位精度方面展 的最优位置（个体最优，pbest）以及整个群体中所
现出巨大潜力。例如，王加安等 对室内可见光定 有粒子找到的最优位置（全局最优，gbest）。这两个
[6]
[7]
位的改进；杨晶东等 在移动机器人全局定位的应 最优值引导着粒子的移动，旨在找到最佳的解决方
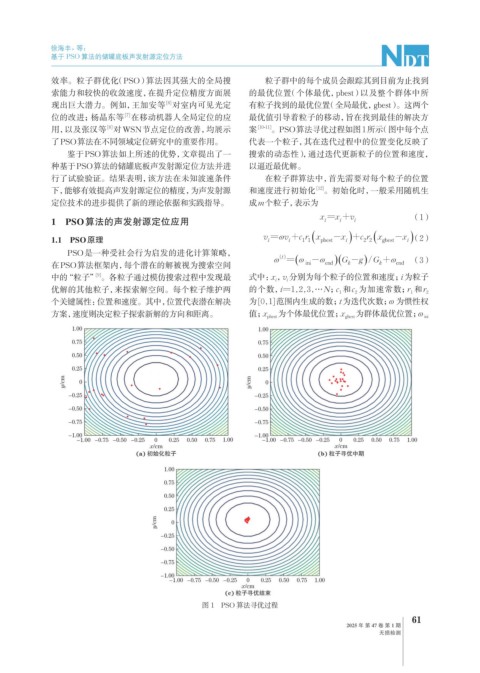
用，以及张汉等 对WSN节点定位的改善，均展示 案 [10-11] 。PSO算法寻优过程如图1所示（图中每个点
[8]
了PSO算法在不同领域定位研究中的重要作用。 代表一个粒子，其在迭代过程中的位置变化反映了
鉴于PSO算法如上所述的优势，文章提出了一 搜索的动态性），通过迭代更新粒子的位置和速度，
种基于PSO算法的储罐底板声发射源定位方法并进 以逼近最优解。
行了试验验证。结果表明，该方法在未知波速条件 在粒子群算法中，首先需要对每个粒子的位置
下，能够有效提高声发射源定位的精度，为声发射源 和速度进行初始化 [12] 。初始化时，一般采用随机生
定位技术的进步提供了新的理论依据和实践指导。 成m个粒子，表示为
x =+v （1）
x
1 PSO算法的声发射源定位应用 i i i
v =ω + v cr - x  +x c r - x x 
1.1 PSO原理 i i 1 1  pbest i 2 2  gbest i （2）
PSO是一种受社会行为启发的进化计算策略， () t
在PSO算法框架内，每个潜在的解被视为搜索空间 = ω  ini - ω ω end  k -G  /g k +G ω end （3）
中的“粒子” 。各粒子通过模仿搜索过程中发现最 式中：x ，v 分别为每个粒子的位置和速度；i为粒子
[9]
i
i
优解的其他粒子，来探索解空间。每个粒子维护两 的个数，i=1,2,3,…N；c 和c 为加速常数；r 和r 2
1
2
1
个关键属性：位置和速度。其中，位置代表潜在解决 为[0,1]范围内生成的数；t为迭代次数；ω 为惯性权
方案，速度则决定粒子探索新解的方向和距离。 值；x pbest 为个体最优位置；x gbest 为群体最优位置；ω ini

图 1 PSO 算法寻优过程
61
2025 年 第 47 卷 第 1 期
无损检测