Page 64 - 无损检测2024年第十期
P. 64
林丛林,等:
基于小波时频分析的疲劳损伤定量表征
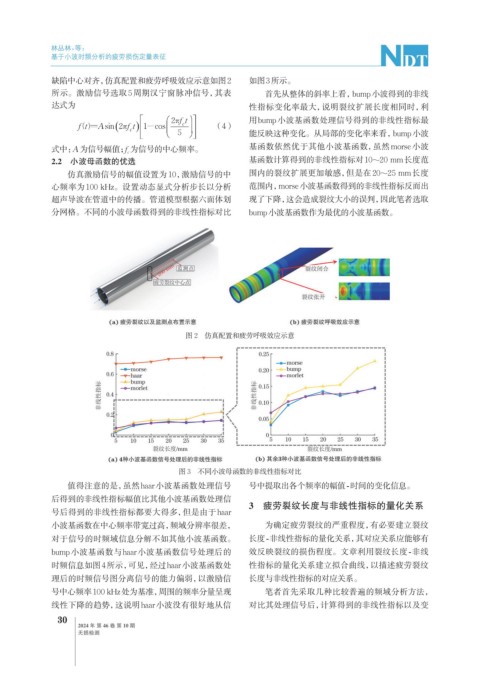
缺陷中心对齐,仿真配置和疲劳呼吸效应示意如图2 如图3所示。
所示。激励信号选取5周期汉宁窗脉冲信号,其表 首先从整体的斜率上看,bump小波得到的非线
达式为 性指标变化率最大,说明裂纹扩展长度相同时,利
用bump小波基函数处理信号得到的非线性指标最
(4)
能反映这种变化。从局部的变化率来看,bump小波
f
式中:A为信号幅值; 为信号的中心频率。 基函数依然优于其他小波基函数,虽然morse小波
c
2.2 小波母函数的优选 基函数计算得到的非线性指标对10~20 mm长度范
仿真激励信号的幅值设置为10,激励信号的中 围内的裂纹扩展更加敏感,但是在20~25 mm长度
心频率为100 kHz。设置动态显式分析步长以分析 范围内,morse小波基函数得到的非线性指标反而出
超声导波在管道中的传播。管道模型根据六面体划 现了下降,这会造成裂纹大小的误判,因此笔者选取
分网格。不同的小波母函数得到的非线性指标对比 bump小波基函数作为最优的小波基函数。
图 2 仿真配置和疲劳呼吸效应示意
图 3 不同小波母函数的非线性指标对比
值得注意的是,虽然haar小波基函数处理信号 号中提取出各个频率的幅值-时间的变化信息。
后得到的非线性指标幅值比其他小波基函数处理信
3 疲劳裂纹长度与非线性指标的量化关系
号后得到的非线性指标都要大得多,但是由于haar
小波基函数在中心频率带宽过高,频域分辨率很差, 为确定疲劳裂纹的严重程度,有必要建立裂纹
对于信号的时频域信息分解不如其他小波基函数。 长度-非线性指标的量化关系,其对应关系应能够有
bump小波基函数与haar小波基函数信号处理后的 效反映裂纹的损伤程度。文章利用裂纹长度-非线
时频信息如图4所示,可见,经过haar小波基函数处 性指标的量化关系建立拟合曲线,以描述疲劳裂纹
理后的时频信号图分离信号的能力偏弱,以激励信 长度与非线性指标的对应关系。
号中心频率100 kHz处为基准,周围的频率分量呈现 笔者首先采取几种比较普遍的频域分析方法,
线性下降的趋势,这说明haar小波没有很好地从信 对比其处理信号后,计算得到的非线性指标以及变
30
2024 年 第 46 卷 第 10 期
无损检测