Page 51 - 无损检测2024年第四期

潘文杰,等:
承压构件缺陷磁记忆检测信号的量化分析

一部分应力能, 使磁晶体内部能量总体上为最小值。
平板处于不同载荷时, 提取不同埋深状态下法
向磁场梯度曲线极大值点处的 K 值作为因变量, 以
拉伸载荷σ 为自变量进行曲线拟合, 拟合曲线如图
5 ( d ) 所示, 拟合公式为
- σ
- 3 90.73 ( 2 )
K =- 8.66×10 ×e +0.01
分析拟合曲线可知, K 与 σ 呈类指数函数关系。
随着拉伸载荷σ 的增大, 法向磁场梯度 K 增大的速
率减小。
3.2 含气孔缺陷分析
3.2.1 气孔缺陷埋深影响分析

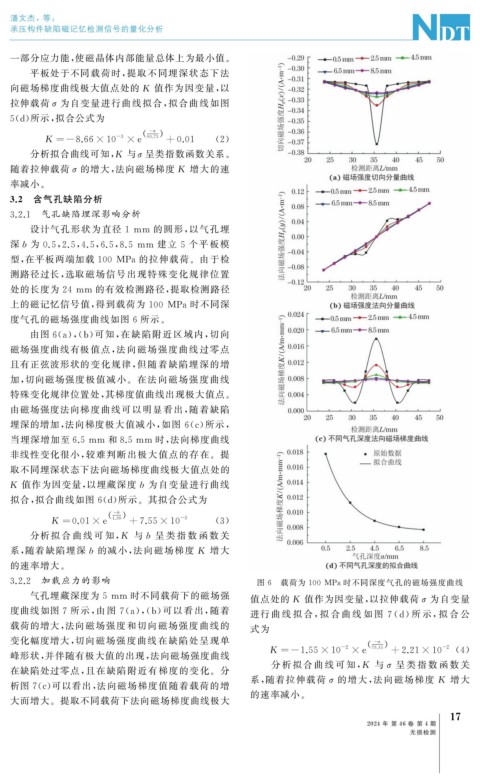
设计气孔形状为直径 1mm 的圆形, 以气孔埋

深b 为 0.5 , 2.5 , 4.5 , 6.5 , 8.5 mm 建立 5 个平板模

型, 在平板两端加载 100 MPa的拉伸载荷。由于检
测路径过长, 选取磁场信号出现特殊变化规律位置

处的长度为 24mm 的有效检测路径, 提取检测路径

上的磁记忆信号值, 得到载荷为 100 MPa时不同深
度气孔的磁场强度曲线如图 6 所示。
由图 6 ( a ),( b ) 可知, 在缺陷附近区域内, 切向
磁场强度曲线有极值点, 法向磁场强度曲线过零点
且有正弦波形状的变化规律, 但随着缺陷埋深的增
加, 切向磁场强度极值减小。在法向磁场强度曲线
特殊变化规律位置处, 其梯度值曲线出现极大值点。
由磁场强度法向梯度曲线可以明显看出, 随着缺陷
埋深的增加, 法向梯度极大值减小, 如图 6 ( c ) 所示,

当埋深增加至6.5mm 和8.5mm 时, 法向梯度曲线
非线性变化很小, 较难判断出极大值点的存在。提
取不同埋深状态下法向磁场梯度曲线极大值点处的
K 值作为因变量, 以埋藏深度b 为自变量进行曲线
拟合, 拟合曲线如图 6 ( d ) 所示。其拟合公式为
- b
1.99
K = 0.01×e +7.55×10 - 3 ( 3 )
分析 拟 合 曲 线 可 知, K 与b 呈 类 指 数 函 数 关
系, 随着缺陷埋深b 的减小, 法向磁场梯度 K 增大
的速率增大。
3.2.2 加载应力的影响 图 6 载荷为 100 MPa时不同深度气孔的磁场强度曲线

气孔埋藏深度为 5mm 时不同载荷下的磁场强 值点处的 K 值作为因变量, 以拉伸载荷σ 为自变量
度曲线如图 7 所示, 由图 7 ( a ),( b ) 可以看出, 随着 进行 曲 线 拟 合, 拟 合 曲 线 如 图 7 ( d ) 所 示, 拟 合 公
载荷的增大, 法向磁场强度和切向磁场强度曲线的 式为
变化幅度增大, 切向磁场强度曲线在缺陷处呈现单 - σ
- 2 79.45 - 2 ( 4 )
峰形状, 并伴随有极大值的出现, 法向磁场强度曲线 K =- 1.55×10 ×e +2.21×10
分 析 拟 合 曲 线 可 知, K 与σ 呈 类 指 数 函 数 关
在缺陷处过零点, 且在缺陷附近有梯度的变化。分
系, 随着拉伸载荷σ 的增大, 法向磁场梯度 K 增大
析图 7 ( c ) 可以看出, 法向磁场梯度值随着载荷的增
的速率减小。
大而增大。提取不同载荷下法向磁场梯度曲线极大
7
1
2024 年 第 46 卷 第 4 期
无损检测