Page 79 - 无损检测2023年第九期
P. 79
安 康, 等:
基于微波时间反演算法的复合材料内部损伤检测
信号经过多个散射体的多次散射后得到的散射信 在于可以更加直观地观察在时间反演过程中电磁场
号, 直接对该散射信号进行时间反转和回传无法 的变化规律, 有利于更好地对时间反演算法的聚焦
使其在目标位置聚焦。因此, 为了获得与目标相 过程进行分析。
关的散射信号, 需要采用背景相消法 [ 21 ] , 即对健康 在微波时间反演算法中, 脉冲宽度决定了算法
模型的散射信号进行测量, 并将其作为参考信号。 的纵向分辨率, 因此, 通常采用短微波脉冲信号作为
在对损伤模型进行测量时, 将测量得到的散射信 信号源。文章采用高斯调制脉冲作为微波脉冲源,
号减去参考信号, 以得到与待测目标相关的散射 表达式如下
信号, 并将该信号称为扰动信号。通过将扰动信 2
t - t
- 0
号在时间上进行反转, 并回传到原健康模型中, 时 s ( t ) e τ 2 cos ( 2π f c t ) ( 2 )
=
间反转后的扰动信号会自适应地在待测目标处实 式中: 中 心 频 率 f c 为 20 GHz ( 对 应 波 长 λ 为
现聚焦。这一理论为时间反演算法在无损检测中 15mm ); 影响脉冲带宽的参数 τ 为20p s ; 微波脉冲
的应用奠定了理论基础。 信号的时间延迟 t 0 为0.1ns 。
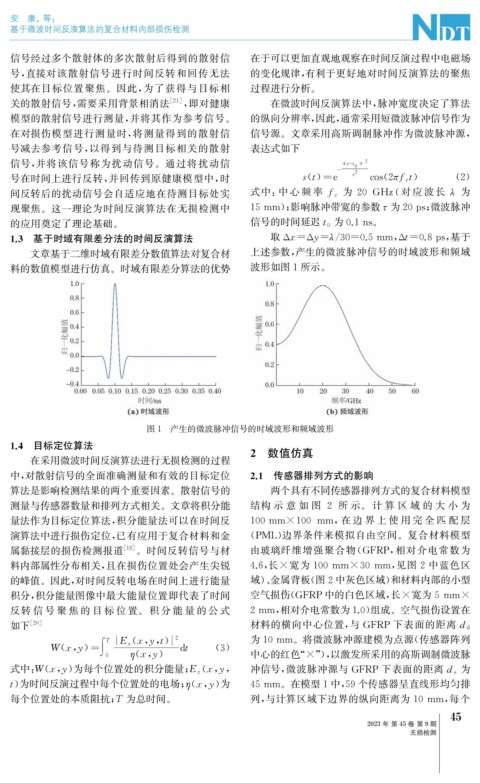
1.3 基于时域有限差分法的时间反演算法 取 Δx=Δ y=λ / 30=0.5mm , Δ t=0.8p s , 基于
文章基于二维时域有限差分数值算法对复合材 上述参数, 产生的微波脉冲信号的时域波形和频域
料的数值模型进行仿真。时域有限差分算法的优势 波形如图1所示。
图1 产生的微波脉冲信号的时域波形和频域波形
1.4 目标定位算法 2 数值仿真
在采用微波时间反演算法进行无损检测的过程
中, 对散射信号的全面准确测量和有效的目标定位 2.1 传感器排列方式的影响
算法是影响检测结果的两个重要因素。散射信号的 两个具有不同传感器排列方式的复合材料模型
测量与传感器数量和排列方式相关。文章将积分能 结构 示 意 如 图 2 所 示。 计 算 区 域 的 大 小 为
量法作为目标定位算法, 积分能量法可以在时间反 100mm×100 mm , 在 边 界 上 使 用 完 全 匹 配 层
演算法中进行损伤定位, 已有应用于复合材料和金 ( PML ) 边界条件来模拟自由空间。复合材料模型
属黏接层的损伤检测报道 [ 18 ] 。时间反转信号与材 由玻璃纤维增强聚合物( GFRP , 相对介电常数为
料内部属性分布相关, 且在损伤位置处会产生尖锐 4.6 , 长× 宽为 100mm×30mm , 见图 2 中蓝色区
的峰值。因此, 对时间反转电场在时间上进行能量 域)、 金属背板( 图2中灰色区域) 和材料内部的小型
积分, 积分能量图像中最大能量位置即代表了时间 空气损伤( GFRP中的白色区域, 长×宽为5mm×
反转 信 号 聚 焦 的 目 标 位 置。积 分 能 量 的 公 式 2mm , 相对介电常数为1.0 ) 组成。空气损伤设置在
如下 [ 20 ] 材料的横向中心位置, 与 GFRP 下表面的距离 d d
T E z x , ,) 2 为10mm 。将微波脉冲源建模为点源( 传感器阵列
(
yt
W ( x , ) ∫ η x , ) dt ( 3 ) 中心的红色“ × ”), 以激发所采用的高斯调制微波脉
y =
y
(
0
式中: W ( x , ) 为每个位置处的积分能量; E z x , , 冲信号, 微波脉冲源与 GFRP 下表面的距离d s 为
(
y
y
t ) 为时间反演过程中每个位置处的电场;( x , ) 为 45mm 。在模型1中, 59个传感器呈直线形均匀排
y
η
每个位置处的本质阻抗; T 为总时间。 列, 与计算区域下边界的纵向距离为10mm , 每个
5
4
2023年 第45卷 第9期
无损检测