Page 58 - 无损检测2023年第四期

杨志军, 等:

电梯曳引钢带钢丝不同截面积损伤的漏磁检测

为门槛阈值; ^ ( n ) 为信号阈值化后的小波细节
( = ∑ h ( k-2n ) C j k ) t l d l
C j + 1 n )
(

k∈ Z

( 1 ) 系数。
(
(
D j + 1 n )

( = ∑ g k-2n ) C j k ) 经过软阈值滤波之后, 可利用式( 2 ) 进行小波重

k∈ Z
小波重构算法可表示为 构得到滤波之后的信号。
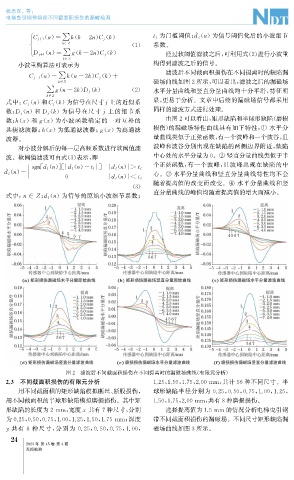
滤波后不同截面积损伤在不同提离时的缺陷漏
(
(
C j - 1 n ) = ∑ h ( n-2k ) C j k ) +
k∈ Z 磁场曲线如图2所示, 可以看出, 滤波之后的漏磁场
(
(
∑ g n-2k ) D j k ) ( 2 ) 水平分量曲线和竖直分量曲线均十分平滑, 特征明
k∈ Z
式中: C j n ) 和C j k ) 为信号在尺寸 上的近似系 显, 更易于分析。文章中后续的漏磁场信号都采用
(
(
j
数; D j n ) 和 D j k ) 为信号在尺寸 j 上的细节系 同样的滤波方式进行处理。
(
(
数; h ( x ) 和 ( x ) 为小波函数确定的一对互补的 由图2可以看出, 矩形缺陷和半球形缺陷( 磨损
g

共轭滤波器; h ( x ) 为低通滤波器; ( x ) 为高通滤 损伤) 的漏磁场特性曲线具有如下特性: ① 水平分
g
量曲线类似于正弦函数, 有一个波峰和一个波谷, 且
波器。
对小波分解后的每一层高频系数进行软阈值滤 波峰和波谷分别出现在缺陷的两侧边界附近, 缺陷

波。软阈值滤波可由式( 3 ) 表示, 即 中心处的水平分量为0 。 ② 竖直分量曲线类似于半
个正弦函数, 有一个波峰, 且波峰出现在缺陷的中
s g n [ d l n () ] d l n > t l
()
()][ d l n - t l
^ ( n ) =
0 d l n < t l
d l 心。 ③ 水平分量曲线和竖直分量曲线特性均不会
()
随着提离值的改变而改变。 ④ 水平分量曲线和竖

( 3 )
直分量曲线的峰值均随着提离值的增大而减小。
式中: n ∈Z ; d l n ) 为信号的原始小波细节系数;
(

图2 滤波后不同截面积损伤在不同提离时的漏磁场曲线( 有限元分析)
2.3 不同截面积损伤的有限元分析 1.25 , 1.50 , 1.75 , 2.00mm , 共计56种不同尺寸。半

用不同截面积的矩形缺陷模拟断丝、 断股损伤, 球形缺陷半径分别为 0.25 , 0.50 , 0.75 , 1.00 , 1.25 ,
用不同截面积的半球形缺陷模拟磨损损伤。其中矩 1.50 , 1.75 , 2.00mm , 共有8种磨损损伤。

形缺陷的长度为2mm , 宽度x 共有7种尺寸, 分别 选择提离值为1.5mm 的情况分析电梯曳引钢

为0.25 , 0.50 , 0.75 , 1.00 , 1.25 , 1.50 , 1.75mm ; 深度 带不同截面积损伤的漏磁场。不同尺寸矩形缺陷漏
y 共有 8 种尺寸, 分别为 0.25 , 0.50 , 0.75 , 1.00 , 磁场曲线如图3所示。
4
2
2023年 第45卷 第4期
无损检测