Page 80 - 无损检测2022年第十一期

艾子微, 等:

B 型套筒搭接角焊缝的兰姆波散射分析

内部。尽管如此, 从长远来看, 内部环焊缝的缺陷仍 和 T 型角 焊 缝 [ 6 ] 的 兰 姆 波 散 射 进 行 了 研 究, 但 B
然威胁着整个结构的安全。研究表明, 若缺陷为裂 型套筒结 构 中 搭 接 角 焊 缝 的 研 究 较 少, 而 通 常 采
纹, 套筒结构的强度接近于管道母材; 而对于完全断 用的研究 方 法 需 要 建 立 二 维 模 型 进 行 数 值 模 拟,
裂, 套筒角焊缝所能承受的最大弯矩约为管道母材 为了避免 模 型 边 界 对 声 场 计 算 的 影 响, 这 些 模 型
[ 4 ] 。因此套筒之下的母材环焊缝内部缺陷 构 建 相 当 复 杂, 且 计 算 时 间 也 相 对 比 较 长 [ 7-9 ] , 在
的69.4%
的发展状况依然是无损检测人员必须关心的问题。 需要对不 同 入 射 模 式 作 用 下, 各 种 尺 寸 及 形 状 管
由于套筒和原管道之间的空气层阻挡了径向波 段的内部声场进行大量计算时并不方便。因此文
的传播, 除了操作管道爬行器从内部进行检测之外, 章希望利 用 变 厚 度 板 [ 10 ] 和 分 层 结 构 [ 11 ] 中 导 波 散
利用兰姆波沿管道进行外部检测可能是一个更为简 射问题的 已 有 理 论, 开 发 基 于 一 维 解 析 解 的 模 式
单、 成本更低的检测方式, 但首先需要解决的问题是 匹配求解方法。
入射兰姆波有多少能量通量及以何种模式通过搭接
角焊缝进入管道母材。只有进入母材的声波才能与 1 基于模式展开法的散射矩阵求解方法
裂纹等缺陷发生交互作用, 并携带缺陷信息通过角 为了便于分析, 将含有搭接填充焊缝的结构等
焊缝被外部传感器所接收。作为兰姆波检测方案的 效为两部分———由波导 1 和 2 构成的变厚度板和波
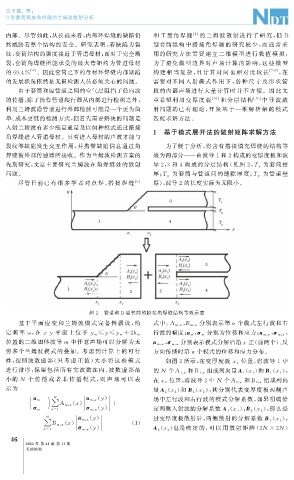
先期研究, 文章主要研究兰姆波在角焊缝处的散射 导 2 , 3 和 4 构成的分层结构( 见图 2 , T s 为套筒壁

问题。 厚; T g 为套筒与管道间的缝隙厚度; T p 为管道壁
尽管目 前 已 有 很 多 学 者 对 点 焊、 搭 接 焊 缝 [ 5 ] 厚), 波导 2 的长度实际为无限小。

图 2 管道和 B 型套筒的搭接角焊缝结构等效示意
基于 平 面 应 变 和 兰 姆 波 模 式 完 备 性 假 设, 给 式中: A m , n B m , n 分别表示第n 个模式左行波和右
,
, , ,
定 频 率 ω , 在 x- y 平 面 上 位 于 y m ≤y≤y m +2h m 行波的幅度; u m σ m 分别为位移和应力; u m , n σ m , n
位置的二维固体波导 m 中任意声场可以分解为无 ~ , ~ 分别表示模式分解后沿x 正( 前两个)、 反
u m , n σ m , n

穷多个兰姆波模式的叠加。考虑到计 算 上 的 可 行 方向传播时第n 个模式的位移和应力分布。
性, 按照波数虚部 ( 只 考 虑 正 值) 大 小 将 这 些 模 式 位置, 将波导 1 中
如图 2 所示, 在变厚度板 x 1
进行排序, 保留包括所有实波数在内、 波数虚部最 的 N 个A 1 , n 和B 1 , n 组成列向量A 1 x 1 ( ),
( ) 和B 1 x 1
小的 N 个 传 播 或 者 非 传 播 模 式, 则 声 场 可 以 表 组成列向
在x 2 位置, 将波导 2 中 N 个A 2 , n 和B 2 , n
示为 ( ), 其分别代表变厚度板两侧声
( ) 和 B 2 x 2
量A 2 x 2
N ( ) 场中左行波和右行波的模式分解系数, 如果明确给
u m , n y
u m
= n=1 A m , n x ) σ m , n y + 定两侧入射波的分解系数 A 1 x 1 B 2 x 2
(
∑
( ), ( ), 那么经
( )

σ m

N ~ ( )
( ),
u m , n y
过变厚度板散射后, 两侧散射的分解系数 B 1 x 1
(
∑ B m , n x ) ~ ( 1 )
( ) 也是确 定 的, 可 以 用 散 射 矩 阵 ( 2 N ×2N )
σ m , n y
n= 1 ( ) A 2 x 2

6
4
2022 年 第 44 卷 第 11 期

无损检测