Page 44 - 无损检测2022年第四期
P. 44
王 瑶,等:
压力容器模拟缺陷的声发射定位
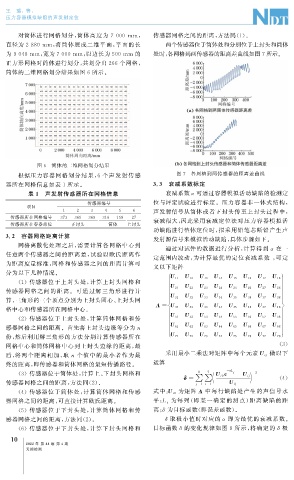
对筒体进行网格划分, 筒体高度为 7000 mm , 传感器网格之间的距离, 方法同( 1 )。
直径为 2880mm , 将筒体展成二维平面, 平面的长 两个传感器位于筒体处和分别位于上封头和筒体
为 9048mm , 宽为7000mm , 以边长为500mm 的 处时, 各网格到两传感器的距离差曲线如图7所示。
正方形网格对筒体进行划分, 共划分出 266 个网格,
筒体的二维网格划分结果如图 6 所示。
图 6 筒体的二维网格划分结果
根据压力容器网格划分结果, 6 个声发射传感 图 7 各网格到两传感器的距离差曲线
器所在网格信息如表 1 所示。 3.3 衰减系数标定
表 1 声发射传感器所在网格信息 衰减系数α 可通过容器模拟活动缺陷的检测定
传感器编号 位与评定试验进行标定。压力容器非一体式结构,
项目
1 2 3 4 5 6 声发射信号从筒体或者下封头传至上封头过程中,
传感器所在网格编号 373 365 369 316 158 27 衰减很大, 因此采用衰减定位法对压力容器模拟活
传感器所在容器部位 下封头 筒体 上封头
动缺陷进行整体定位时, 拟采用铅笔芯断铅产生声
3.2 容器网格距离计算 发射源信号来模拟活动缺陷, 具体步骤如下。
网格离散化处理之后, 需要计算各网格中心到 通过对试件的数据进行分析, 计算得到α 在一
任意两个传感器之间的距离差, 试验以欧氏距离作
定范围内波动, 为计算最优的定位衰减系数 , 可定
为距离度量标准, 网格和传感器之间的距离计算可
义以下矩阵
分为以下几种情况。
U 11 U 12 U 13 U 14 U 15 U 16 U 17 U 18
( 1 )传感器位于上封头处, 计算上封头网格和
传感器网格之间的距离。可通过解三角形 进行计 U 21 U 22 U 23 U 24 U 25 U 26 U 27 U 28
算, 三角形的三个顶点分别为上封头圆心、 上封头网 U 31 U 32 U 33 U 34 U 35 U 36 U 37 U 38
A = U 41 U 42 U 43 U 44 U 45 U 46 U 47 U 48
格中心和传感器所在网格中心。
( 2 )传感器位于上封头处, 计算筒体网格和传 U 51 U 52 U 53 U 54 U 55 U 56 U 57 U 58
感器网格之间的距离。首先将上封头边缘等分为n U 61 U 62 U 63 U 64 U 65 U 66 U 67 U 68
份, 然后利用解三角形的方法分别计算传感器所在
U 71 U 72 U 73 U 74 U 75 U 76 U 77 U 78
网格中心和筒体网格中心到上封头边缘的距离, 最 ( 3 )
后, 将两个距离相加, 取 n 个值中的最小者作为最 采用最小二乘法对矩阵中每个元素U i j 做以下
终的距离, 即传感器和筒体网格的最短传播路径。 运算
- αL
( 3 )传感器位于筒体处, 计算上、 下封头网格和 8 7 U i0 e j -U i j 2
δ= ∑∑ ( 4 )
传感器网格之间的距离, 方法同( 2 )。 j=1 i = 1 U i j
( 4 )传感器位于筒体处, 计算筒体网格和传感 式中: U i0 为矩阵 A 中每行缺陷处产生的声信号水
器网格之间的距离, 可直接计算欧氏距离。 平; L j 为每列 ( 即某一确定的测点) 距离缺陷的距
( 5 )传感器位于下封头处, 计算筒体网格和传 离; δ 为目标函数( 即误差函数)。
感器网格之间的距离, 方法同( 2 )。 δ 取极小值时对应的α 即为最优的衰减系数。
( 6 )传感器位于下封头处, 计算下封头网格和 目标函数δ 的变化规律如图 8 所示, 将确定的δ 极
0
1
2022 年 第 44 卷 第 4 期
无损检测