Page 47 - 无损检测2025年第四期

张 茹，等：

基于压电阻抗技术的工字形钢梁局部损伤识别方法

为了获取损伤定位和损伤定量的有效特征频 迭代计算，确定 max(k /k ) 所在的频段为损伤定位
2
1
段，将电导信号每隔10 kHz作为1个频段区间，计算 的有效特征频段 [ f ，f ]，确定 max(k /k ) 所在的频
2
1
2
1
每个频段区间的R 和R 值。记R 最大值与最小值 段为损伤定量的有效特征频段[ f ，f ]。[ f ，f ]所在
2j
1i
1i
4
3
2
1
的差值为k ，R 最大值与最小值的差值为k 。迭代 频段的电导对损伤程度不敏感，而[ f ，f ]所在频段
2j
2
1
3
4
计算是一种逐次逼近最优解的数值计算方法。文 的电导信号对损伤位置不敏感。因此，在[ f ，f ]内
1 2
章通过递归评估每个频段k 与k 之间的比值，以每 拟合 R 与损伤位置 d 的线性关系，用于损伤定位。
1
2
1
个频段中k 与k 间的比值为迭代，系统地逼近这两 在[ f ，f ]内获得R 随损伤长度l的变化规律，用于
3
4
2
2
1
个比值的最大值，即max(k /k )和max(k /k )。通过 损伤定量。其具体流程如图2所示。
1 2 2 1

图 2 基于有效频段选取的损伤识别流程图
实际检测过程中，假设损伤位于PZT m和PZT n
之间，PZT m和PZT n的距离为L，二者与损伤的
距离分别为L 和L 。由于损伤位置不确定，故联合
m
n
PZT m和PZT n的电导信号修正R 2 值，并代入标定
试验得到的距离损伤为L的压电片的R -l曲线中，
2
计算损伤长度l。R 2 的修正公式为

（4）

式中： R 2 （m）和R 2 （n）分别为通过PZT m和PZT n
测得的当前损伤程度下的R 2 值。
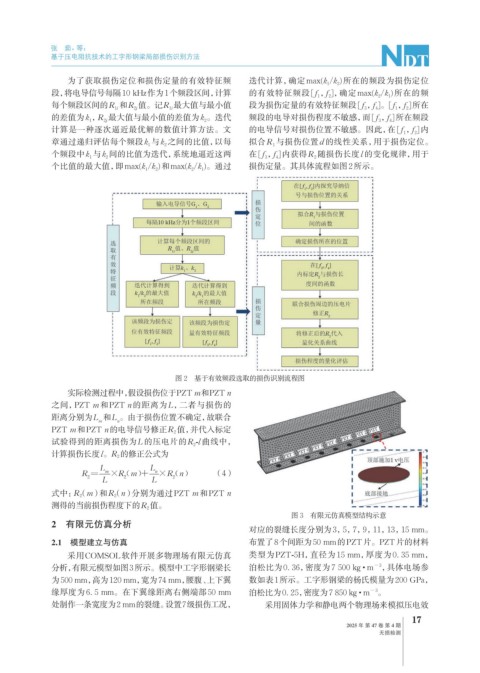
图 3 有限元仿真模型结构示意
2 有限元仿真分析
对应的裂缝长度分别为3，5，7，9，11，13，15 mm。
2.1 模型建立与仿真 布置了8个间距为50 mm的PZT片。PZT片的材料
采用COMSOL软件开展多物理场有限元仿真 类型为PZT-5H，直径为 15 mm，厚度为 0. 35 mm，
分析，有限元模型如图3所示。模型中工字形钢梁长 泊松比为0. 36，密度为7 500 kg · m ，具体电场参
−3
为500 mm，高为120 mm，宽为74 mm，腰腹、上下翼 数如表1所示。工字形钢梁的杨氏模量为200 GPa，
−3
缘厚度为6. 5 mm。在下翼缘距离右侧端部50 mm 泊松比为0. 25，密度为7 850 kg · m 。
处制作一条宽度为2 mm的裂缝。 设置7级损伤工况， 采用固体力学和静电两个物理场来模拟压电效
17
2025 年 第 47 卷 第 4 期
无损检测