Page 39 - 无损检测2023年第八期
P. 39
陈冬冬, 等:
基于时间反转算法和归一化小波能量熵的套筒灌浆缺陷检测
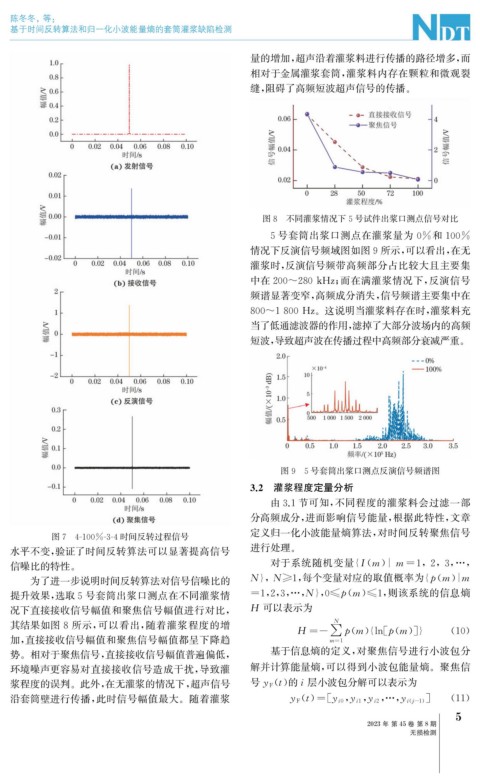
量的增加, 超声沿着灌浆料进行传播的路径增多, 而
相对于金属灌浆套筒, 灌浆料内存在颗粒和微观裂
缝, 阻碍了高频短波超声信号的传播。
图8 不同灌浆情况下5号试件出浆口测点信号对比
5号套筒出浆口测点在灌浆量为 0% 和 100%
情况下反演信号频域图如图9所示, 可以看出, 在无
灌浆时, 反演信号频带高频部分占比较大且主要集
中在200~280kHz ; 而在满灌浆情况下, 反演信号
频谱显著变窄, 高频成分消失, 信号频谱主要集中在
800~1800Hz 。这说明当灌浆料存在时, 灌浆料充
当了低通滤波器的作用, 滤掉了大部分波场内的高频
短波, 导致超声波在传播过程中高频部分衰减严重。
图9 5号套筒出浆口测点反演信号频谱图
3.2 灌浆程度定量分析
由3.1节可知, 不同程度的灌浆料会过滤一部
分高频成分, 进而影响信号能量, 根据此特性, 文章
图7 4-100%-3-4时间反转过程信号 定义归一化小波能量熵算法, 对时间反转聚焦信号
水平不变, 验证了时间反转算法可以显著提高信号 进行处理。
信噪比的特性。 对于系统随机变量{ I ( m ) |m=1 , 2 , 3 ,…,
为了进一步说明时间反转算法对信号信噪比的 N }, N≥1 , 每个变量对应的取值概率为{ ( m ) |m
p
(
提升效果, 选取5号套筒出浆口测点在不同灌浆情 =1 , 2 , 3 ,…, N }, 0≤ p m ) ≤1 , 则该系统的信息熵
况下直接接收信号幅值和聚焦信号幅值进行对比, H 可以表示为
其结果如图 8 所示, 可以看出, 随着灌浆程度的增 N
(
p
H =- ∑ p m ){ ln [ ( m )]} ( 10 )
加, 直接接收信号幅值和聚焦信号幅值都呈下降趋 m= 1
基于信息熵的定义, 对聚焦信号进行小波包分
势。相对于聚焦信号, 直接接收信号幅值普遍偏低,
环境噪声更容易对直接接收信号造成干扰, 导致灌 解并计算能量熵, 可以得到小波包能量熵。聚焦信
浆程度的误判。此外, 在无灌浆的情况下, 超声信号 号 y Ft 的 i 层小波包分解可以表示为
()
沿套筒壁进行传播, 此时信号幅值最大。随着灌浆 y Ft = y i0 y i1 y i2 y ij ( 11 )
() [ , , ,…, ( - 1 ) ]
5
2023年 第45卷 第8期
无损检测