Page 37 - 无损检测2022年第十期
P. 37
李孟奇,等:
金属小径管外壁裂纹的内检式电磁超声导波检测
0.27 。在管件外壁设置裂纹, 其位置和尺寸参数( 包 较窄的时域宽度, 最终确定式( 1 ) 中的 n 为 5 , 为
f
括轴向宽度a 、 周向长度b 和径向深度h ) 可变, 用 250kHz , A 为 1 。 在确定激励信号中心频率和波
于分析计算不同位置、 不同尺寸裂纹对检测信号的 形后, 考虑到感应涡流集中分布于管件内壁, 与薄壁
影响规律。综合考虑有限元计算速度和精度, 采用 线圈组中的涡流线圈个数及位置对应, 在被测管件
四面体单元对管件进行网格划分, 在裂纹缺陷区域 内壁处选取一组环形激励面, 将主方向为轴向且波
进行网格加密, 提高计算精度。 形为式( 1 ) 所定义的瞬时力施加在激励面上, 通过瞬
1.3 激励信号选择及加载方式 态动力学仿真计算, 获取信号拾取位置处( 轴向位置
在进行管件内检式电磁超声导波检测之前, 为 为薄壁线圈组中心; 径向位置为管件内壁) 的质点纵
抑制所激发的超声导波出现频散现象, 应对激励信 向位移信号, 因为该信号与薄壁线圈组输出的电动
号中心频率和波形进行择优选取, 将管件的几何和 势信号正相关, 所以在仿真中以质点纵向位移信号
物理参数代入频散方程中, 计算得到 2205 不锈钢中 来表征检测信号, 用于信号特性分析。
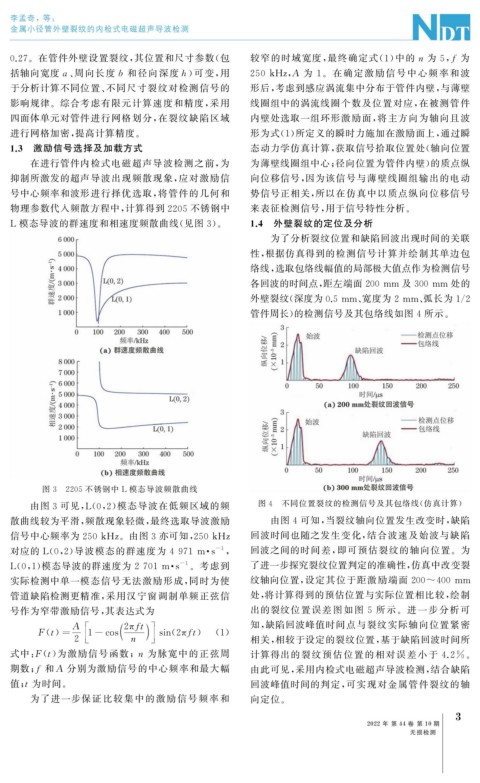
L 模态导波的群速度和相速度频散曲线( 见图 3 )。 1.4 外壁裂纹的定位及分析
为了分析裂纹位置和缺陷回波出现时间的关联
性, 根据仿真得到的检测信号计算并绘制其单边包
络线, 选取包络线幅值的局部极大值点作为检测信号
各回波的时间点, 距左端面 200mm 及 300mm 处的
外壁裂纹( 深度为0.5mm 、 宽度为 2mm 、 弧长为 1 / 2
管件周长) 的检测信号及其包络线如图 4 所示。
图 3 2205 不锈钢中 L 模态导波频散曲线
由图 3 可见, L ( 0 , 2 ) 模态导波在低频区域的频 图 4 不同位置裂纹的检测信号及其包络线( 仿真计算)
散曲线较为平滑, 频散现象轻微, 最终选取导波激励 由图 4 可知, 当裂纹轴向位置发生改变时, 缺陷
信号中心频率为 250kHz 。由图3 亦可知, 250kHz 回波时间也随之发生变化, 结合波速及始波与缺陷
对应的 L ( 0 , 2 ) 导波模态的群速度为 4971m · s , 回波之间的时间差, 即可预估裂纹的轴向位置。为
-1
L ( 0 , 1 ) 模态导波的群速度为 2701m · s 。考虑到 了进一步探究裂纹位置判定的准确性, 仿真中改变裂
-1
实际检测中单一模态信号无法激励形成, 同时为使 纹轴向位置, 设定其位于距激励端面 200~400mm
管道缺陷检测更精准, 采用汉宁窗调制单频正弦信 处, 将计算得到的预估位置与实际位置相比较, 绘制
号作为窄带激励信号, 其表达式为 出的裂纹位置误差图如图 5 所示。进一步分析可
知, 缺陷回波峰值时间点与裂纹实际轴向位置紧密
2π f t
A
F ( t ) = 1-cos n sin ( 2π f t ) ( 1 )
2 相关, 相较于设定的裂纹位置, 基于缺陷回波时间所
式中: F ( t ) 为激励信号函数; n 为脉宽中的正弦周 计算得出的裂纹预估位置的相对误差小于 4.2% 。
期数; 和A 分别为激励信号的中心频率和最大幅 由此可见, 采用内检式电磁超声导波检测, 结合缺陷
f
值; t 为时间。 回波峰值时间的判定, 可实现对金属管件裂纹的轴
为了进一步保证比较集中的激励信号频率和 向定位。
3
2022 年 第 44 卷 第 10 期
无损检测