Page 90 - 无损检测2022年第四期
P. 90
朱高亮,等:
基于有限元分析的压力容器损伤阵列稀疏特征建模与定位方法
) ( 3 )
Δt≤1 /( 20 fmax
式中: 为频带中频率的最大值。
fmax
综合考虑, 笔者采用的中心频率为 90kHz , 其
对应的波长为17.47mm , 在有限元模型中网格划分
的尺寸为 1mm , 时间步长设置为 0.1 μ s , 满足最小
尺寸网格划分和最短时间步长的要求。
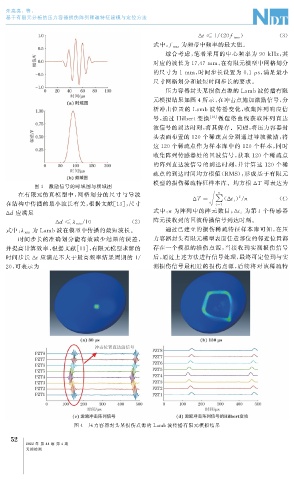
压力容器封头某损伤点源的 Lamb波传播有限
元模拟结果如图 4 所示, 在冲击点施加激励信号, 分
析冲击位置的 Lamb 波传播变化, 收集阵列响应信
号, 通过 Hilbert变换 [ 14 ] 做包络曲线获取阵列直达
波信号的到达时刻, 将其保存。同理, 将压力容器封
头表面布置的 120 个稀疏点分别通过导波激励, 将
这 120 个稀疏点作为样本库中的 120 个样本, 同时
收集阵列传感器处的回波信号, 获取 120 个稀疏点
的阵列直达波信号的到达时刻, 并计算这 120 个稀
疏点的到达时间均方根值( RMS ), 形成基于有限元
模型的损伤稀疏特征样本库。均方根 Δ T 可表达为
图 3 激励信号的时域图与频域图
在有限元仿真模型中, 网格划分的尺寸与导波 n
2
ΔT = ∑ ( Δt i )/ n ( 4 )
在结构中传播的最小波长有关, 根据文献[ 13 ], 尺寸 i =1
Δd 应满足 式中: n 为阵列中的阵元数目; Δt i 为第 i 个传感器
/
Δd ≤λ min 10 ( 2 ) 阵元接收到的回波传播信号到达时刻。
为 Lamb波在模型中传播的最短波长。 通过已建立的损伤稀疏特征样本库可知, 在压
式中: λ min
时间步长的准确划分能有效减少结果的误差, 力容器封头有限元模型表面任意部位的邻近位置都
并提高计算效率, 根据文献[ 13 ], 有限元模型求解的 存在一个模拟的损伤点源, 当接收到实测损伤信号
时间步长 Δ t 应满足不大于最高频率结果周期的 1 / 后, 通过上述方法进行信号处理, 最终可定位到与实
20 , 可表示为 测损伤信号最相近的损伤点源, 后续将对该稀疏特
图 4 压力容器封头某损伤点源的 Lamb波传播有限元模拟结果
5
2
2022 年 第 44 卷 第 4 期
无损检测