Page 110 - 无损检测2021年第八期

于全朋, 等:

飞机关键部件结冰的超声导波探测

行结冰探测是可行的。
1 半解析有限元法求解超声导波传播规律
表 1 明冰的材料参数
将带有积冰的飞机部件简化为冰 - 基底两层平 密度 / 拉梅常数 拉梅常数
杨氏模量 / GPa 泊松比
/
板结构, 积冰为各向同性材料, 基底为金属铝材料, ( g · cm -3 ) λ / GPa μ GPa
冰 - 铝板有限元模型如图 1 所示。 0.9 8.3 0.351 7.24 3.07

图 1 冰 - 铝板有限元模型
固体中的弹性波符合以下 Navier控制方程

··
)
y
(,
( λ+ μ u j , i j + μ u i , jj = ρ u i i j= x , , z )( 1 )

式中: λ 和 μ 为拉梅常数; u 为位移; u i 为位移的二
··
阶导数; 为密度; x , , z 为坐标轴; i 为自由指标;
y
ρ
为位移的 Christoffel符号。
j 为哑指标; u j , i j 和u i , jj
将三维模型简化为二维模型, x 方向为波传播
方向, z 方向为厚度方向, 沿波导介质传播方向的位
移用简谐波振动方式表示为
=
u ( x , z , t ) U ( z ) e i ( kx - ωt ) ( 2 )
式中: ω 为角频率; k 为波数; t 为时间; u 为关于x ,
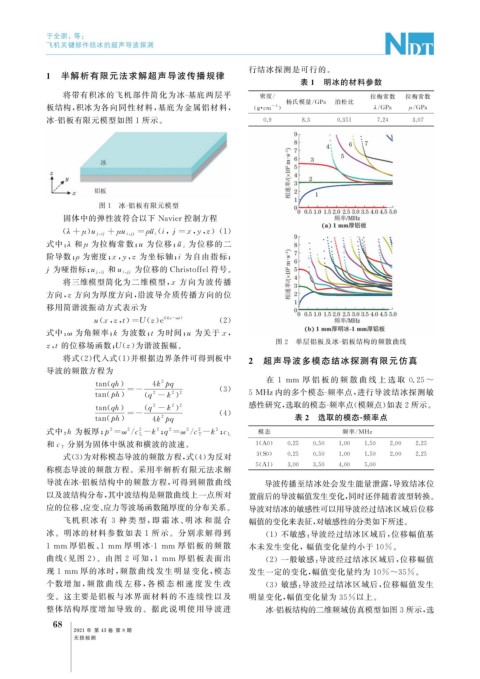
图 2 单层铝板及冰 - 铝板结构的频散曲线
z , t 的位移场函数; U ( z ) 为谐波振幅。
将式( 2 ) 代入式( 1 ) 并根据边界条件可得到板中 2 超声导波多模态结冰探测有限元仿真
导波的频散方程为

2
tan ( h ) 4kpq 在 1 mm 厚 铝 板 的 频 散 曲 线 上 选 取 0.25~
q
=- ( 3 ) 5MHz内的多个模态 - 频率点, 进行导波结冰探测敏

tan ( h ) ( 2 2 2
q -k )
p
q -k )
tan ( h ) ( 2 2 2 感性研究, 选取的模态 - 频率点( 模频点) 如表2所示。
q
=- ( 4 ) 表 2 选取的模态 - 频率点
tan ( h ) 4kpq
p
2
p 2 2 2 2 q 2 2 2 2 模态 频率 / MHz
式中: h 为板厚; =ω / c L-k ; =ω / c T-k ; c L
分别为固体中纵波和横波的波速。 1 ( A0 ) 0.25 0.50 1.00 1.50 2.00 2.25
和c T
式( 3 ) 为对称模态导波的频散方程, 式( 4 ) 为反对 3 ( S0 ) 0.25 0.50 1.00 1.50 2.00 2.25
称模态导波的频散方程。采用半解析有限元法求解 5 ( A1 ) 3.00 3.50 4.00 5.00
导波在冰 - 铝板结构中的频散方程, 可得到频散曲线 导波传播至结冰处会发生能量泄露, 导致结冰位
以及波结构分布, 其中波结构是频散曲线上一点所对 置前后的导波幅值发生变化, 同时还伴随着波型转换。
应的位移、 应变、 应力等波场函数随厚度的分布关系。 导波对结冰的敏感性可以用导波经过结冰区域后位移
飞机积 冰 有 3 种 类 型, 即 霜 冰、 明 冰 和 混 合 幅值的变化来表征, 对敏感性的分类如下所述。
冰。明冰的材料参数如表 1 所示。分别求解得到 ( 1 )不敏感: 导波经过结冰区域后, 位移幅值基

1mm 厚铝板、 1 mm 厚明 冰 -1 mm 厚 铝 板 的 频 散 本未发生变化,幅值变化量约小于 10% 。

曲线( 见图 2 )。由图 2 可知, 1 mm 厚铝板表面出 ( 2 )一般敏感: 导波经过结冰区域后, 位移幅值

现 1mm 厚的冰时, 频散曲线发生明显变化, 模态 发生一定的变化, 幅值变化量约为 10%~35% 。
个数增 加, 频 散 曲 线 左 移, 各 模 态 相 速 度 发 生 改 ( 3 )敏感: 导波经过结冰区域后, 位移幅值发生

变。这主要是铝板与冰界面材料的不连续性以及 明显变化, 幅值变化量为 35% 以上。
整体结构厚度增加导致的。据此说明使用导波进 冰 - 铝板结构的二维频域仿真模型如图3所示, 选
6
8
2021 年 第 43 卷 第 8 期

无损检测