Page 87 - 无损检测2021年第四期

韩 伟, 等:

基于超声 Lamb波的双曲线定位损伤成像方法

模态为主导
该研究以中心频率为 100kHz , A 0
的超声 Lamb 波 为 激 励 信 号, 其 对 应 的 波 长 λ 为
10.9mm , 综合考虑, 有限元仿真中模型的网格尺寸

设置为 1 mm , 时间步长选为 0.01 μ s , 兼顾精度要

求与计算效率。
2.3 双曲线定位方法结果
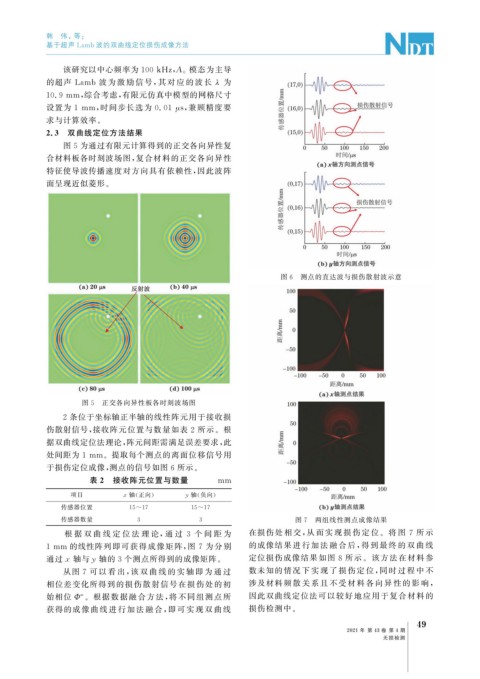
图 5 为通过有限元计算得到的正交各向异性复
合材料板各时刻波场图, 复合材料的正交各向异性
特征使导波传播速度对方向具有依赖性, 因此波阵
面呈现近似菱形。

图 6 测点的直达波与损伤散射波示意

图 5 正交各向异性板各时刻波场图
2 条位于坐标轴正半轴的线性阵元用于接收损
伤散射信号, 接收阵元位置与数量如表 2 所示。根
据双曲线定位法理论, 阵元间距需满足误差要求, 此
处间距为 1mm 。提取每个测点的离面位移信号用

于损伤定位成像, 测点的信号如图 6 所示。
表 2 接收阵元位置与数量 mm
项目 x 轴( 正向) y 轴( 负向)
传感器位置 15~17 15~17
传感器数量 3 3 图 7 两组线性测点成像结果
根 据 双 曲 线 定 位 法 理 论, 通 过 3 个 间 距 为 在损伤处 相 交, 从 而 实 现 损 伤 定 位。 将 图 7 所 示

1mm 的线性阵列即可获得成像矩阵, 图 7 为分别 的成像结 果 进 行 加 法 融 合 后, 得 到 最 终 的 双 曲 线
通过x 轴与 y 轴的 3 个测点所得到的成像矩阵。 定位损伤成像结果如图 8 所示。该方法在材料参
从图 7 可 以 看 出, 该 双 曲 线 的 实 轴 即 为 通 过 数未知的 情 况 下 实 现 了 损 伤 定 位, 同 时 过 程 中 不
相位差变化所得到的损伤散射信号在损伤处的初 涉及材料 频 散 关 系 且 不 受 材 料 各 向 异 性 的 影 响,
ω
始相位 Φ 。根据数据融合方法, 将不同组测点所 因此双曲线定位法可以较好地应用于复合材料的
获得的成 像 曲 线 进 行 加 法 融 合, 即 可 实 现 双 曲 线 损伤检测中。
9
4

2021 年 第 43 卷 第 4 期
无损检测