Page 86 - 无损检测2021年第四期

韩 伟, 等:

基于超声 Lamb波的双曲线定位损伤成像方法

2.1 激励荷载选择与设置
Lamb波在结构中具有多模态特性且受频散效
应的影响, 其信号复杂并难以分析。窄带激励受频
散影响相对较小, 波形畸变不显著, 信号简单且利于
分析。双曲线定位法采用汉宁窗调制的五峰波窄带
信号作为激励信号, 如式( 9 ) 所示。

图 2 双曲线定位损伤成像方法原理示意 S = A 2π f c n
t · sin2π f c , t∈ 0 ,
n
1-cos

单元边界点的相位相关系数即是损伤成像矩阵的像 2 f c

( 9 )
素点, 若该单元边界点为损伤, 则相位相似性高, 在
式中: A 为 激 励 信 号 幅 值; 为 中 心 频 率, 选 取
损伤成像结果中将以较高的像素值重点显示。 f c

100kHz 。
通过式( 7 ) 可分别求得 x 轴与 y 轴两条线性阵
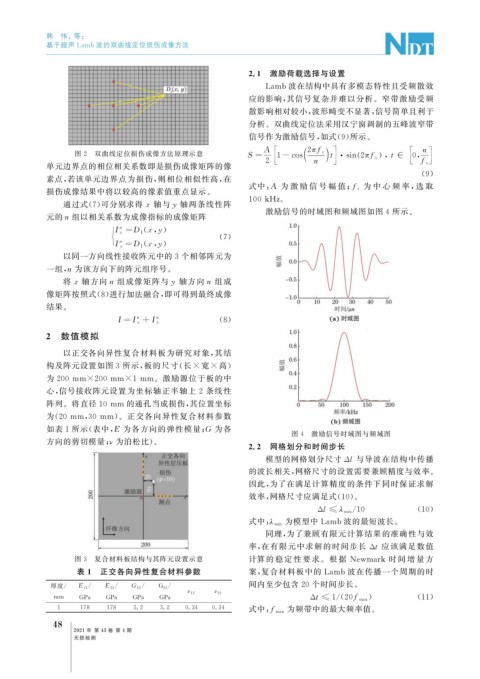
激励信号的时域图和频域图如图 4 所示。
元的n 组以相关系数为成像指标的成像矩阵
n
I x =D I x , )
y
(
n ( y ( 7 )
I y =D I x , )
以同一方向线性接收阵元中的 3 个相邻阵元为
一组, n 为该方向下的阵元组序号。
将x 轴方向n 组成像矩阵与 y 轴方向n 组成
像矩阵按照式( 8 ) 进行加法融合, 即可得到最终成像
结果。
n n ( 8 )
I= I x +I y
2 数值模拟
以正交各向异性复合材料板为研究对象, 其结
构及阵元设置如图 3 所示, 板的尺寸( 长 × 宽 × 高)

为 200mm×200mm×1mm 。激励源位于板的中

心, 信号接收阵元设置为坐标轴正半轴上 2 条线性

阵列。将直径 10mm 的通孔当成损伤, 其位置坐标

为( 20mm , 30mm )。正交各向异性复合材料参数
如表 1 所示( 表中, E 为各方向的弹性模量; G 为各
图 4 激励信号时域图与频域图
方向的剪切模量; ν 为泊松比)。
2.2 网格划分和时间步长
模型的网格划分尺寸 Δl 与导波在结构中传播
的波长相关, 网格尺寸的设置需要兼顾精度与效率。
因此, 为了在满足计算精度的条件下同时保证求解
效率, 网格尺寸应满足式( 10 )。
/
Δl ≤λ min 10 ( 10 )
为模型中 Lamb波的最短波长。
式中: λ min
同理, 为了兼顾有限元计算结果的准确性与效
率, 在有限元中求解的时间步长 Δt 应该满足数值
图 3 复合材料板结构与其阵元设置示意 计算的 稳 定 性 要 求。根 据 Newmark 时 间 增 量 方
表 1 正交各向异性复合材料参数 案, 复合材料板中的 Lamb 波在传播一个周期的时

厚度 / / / / / 间内至少包含 20 个时间步长。
E 11 E 22 G 12 G 23
ν 12 ν 23
mm GPa GPa GPa GPa Δ t≤1 /( 20 fmax ) ( 11 )
1 178 178 5.2 5.2 0.34 0.34 式中: 为频带中的最大频率值。
fmax
8
4

2021 年 第 43 卷 第 4 期

无损检测