Page 79 - 无损检测2021年第四期

赵华民, 等:

厚壁管道轴向裂纹对 C-SH 0 模态反射特性的影响

的相互作用。 MA 等 [ 11 ] 对不同几何形状管道凹痕
与导波反射特性进行了研究。 ZHANG 等 [ 12 ] 采用
有限元方法研究了空心圆柱上圆孔和不同角度的裂
纹缺陷的弯曲模态的反射特性。
周向导波又可分为周向兰姆波( C-Lamb ) 和周
向剪切水平( C-SH ) 波 [ 13 ] 。 ROSE 等 [ 14 ] 研究了各向
同性空心圆柱中水平剪切 SH 波的传播特性, 导出
了频散方程以及沿壁厚方向的位移场和应 力场公

式。 LIU 等 [ 15 ] 通过仿真研究了基于导波周向扫描
和相位特性的管道缺陷定位方法。张小明等 [ 16 ] 研
究了压电圆柱曲面板中的周向导波的复频散特性。
ZHANG 等 [ 17 ] 研究了管道腐蚀和裂纹缺陷的周向
导波检测系统。
以上对周向导波的研究主要集中在其传播特性
上, 而对周向导波与缺陷的相互作用, 特别是定量相
互作用的研究较少。笔者分析了缺陷深度、 缺陷长
度和激励信号参数对周向导波反射系数的影响。研
究了反射信号随裂纹长度、 深度和入射信号频率变
化的关系。为厚壁管道轴向缺陷的快速定量与识别
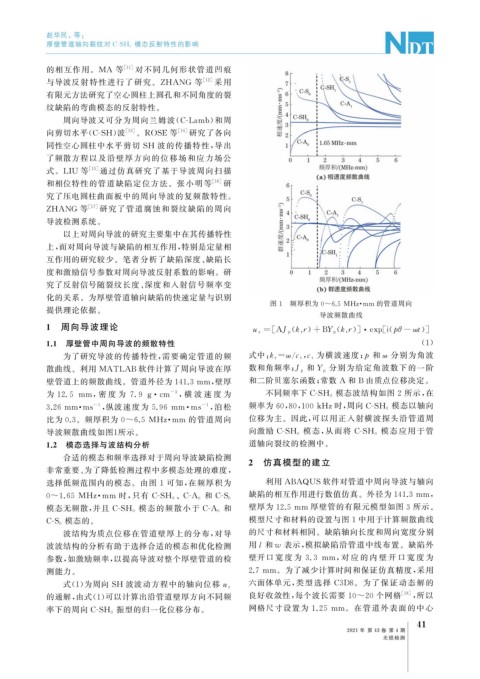
图 1 频厚积为 0~6.5 MHz · mm 的管道周向
提供理论依据。
导波频散曲线
1 周向导波理论 u z = A J p k t r ) +B Y p k t r )] · ex pip θ-ωt )]
(
[(
[
(
1.1 厚壁管中周向导波的频散特性 ( 1 )
, 为横波速度; 和ω 分别为角波
为了研究导波的传播特性, 需要确定管道的频 式中: k t=ω / c t c t p
散曲线。利用 MATLAB 软件计算了周向导波在厚 数和角频率; J p 和Y p 分别为给定角波数下的一阶
壁管道上的频散曲线。管道外径为141.3mm , 壁厚 和二阶贝塞尔函数; 常数 A 和 B 由质点位移决定。

模态波结构如图 2 所示, 在
·
为 12.5 mm , 密 度 为 7.9 g cm -3 , 横 波 速 度 为 不同频率下 C-SH 0

3.26mm · ms , 纵波速度为 5.96 mm · ms , 泊松 频率为 60 , 80 , 100kHz时, 周向 C-SH 0 模态以轴向

-1
-1

比为 0.3 。频厚积为 0~6.5 MHz · mm 的管道周向 位移为主。因此, 可以用正入射横波探头沿管道周
导波频散曲线如图 1 所示。 向激励 C-SH 0 模态, 从而将 C-SH 0 模态应用于管
1.2 模态选择与波结构分析 道轴向裂纹的检测中。
合适的模态和频率选择对于周向导波缺陷检测
2 仿真模型的建立
非常重要。 为了降低检测过程中多模态处理的难度,
选择低频范围内的模态。由图 1 可知, 在频厚积为 利用 ABAQUS 软件对管道中周向导波与轴向

、 缺陷的相互作用进行数值仿真。外径为141.3mm ,
0~1.65 MHz · mm 时, 只有 C-SH 0 C-A 0 和 C-S 0

和 壁厚为 12.5mm 厚壁管的有限元模型如图 3 所示。
模态无频散, 并且 C-SH 0 模态的频散小于 C-A 0
模型尺寸和材料的设置与图 1 中用于计算频散曲线
模态的。
C-S 0
波结构为质点位移在管道壁厚上的分布, 对导 的尺寸和材料相同。缺陷轴向长度和周向宽度分别
波波结构的分析有助于选择合适的模态和优化检测 用l 和w 表示, 模拟缺陷沿管道中线布置。缺陷外

参数, 如激励频率, 以提高导波对整个厚壁管道的检 壁开口 宽 度 为 3.3 mm , 对 应 的 内 壁 开 口 宽 度 为

测能力。 2.7mm 。为了减少计算时间和保证仿真精度, 采用
六面体单元, 类型选择 C3D8 。为了保证动态解的
式( 1 ) 为周向 SH 波波动方程中的轴向位移u z
的通解, 由式( 1 ) 可以计算出沿管道壁厚方向不同频 良好收敛性, 每个波长需要 10~20 个网格 [ 18 ] , 所以

网格尺寸设置为 1.25 mm 。在管道外表面的中心
振型的归一化位移分布。
率下的周向 C-SH 0
1
4

2021 年 第 43 卷 第 4 期

无损检测