Page 100 - 无损检测2021年第四期

刘鹏飞, 等:

基于非线性超声谐波法的混凝土构件应力检测

新的谐波分量。混凝土的早期退化特性, 如微裂隙、 变形前的密度。
微缺陷 等 微 观 结 构 变 化 与 非 线 性 声 学 效 应 密 切 混凝土是一种介于离散介质和连续介质之间的
相关。 材料。从离散模型出发, 假设一列沿 x 轴方向传播
因此, 笔者根据非线性参数调制理论建立有限 的压缩纵波进入混凝土介质中, 结合式( 1 ), 可以得
元仿真模型, 分析该方法对应力检测的敏感性。搭 到离散模型非线性超声纵波波动方程
建了单轴加载非线性超声波应力检测系统, 以不同 ∂u ∂u ∂u∂u
2
2
2
ρ 2 =E ∂x 2 + β ∂x∂x ( 4 )
强度等级的混凝土试样为检测对象, 研究在不同应 ∂t 2
力水平下, 混凝土中传播的超声激励信号与混凝土 E 与纵波声速 c 的关系有
2
裂纹发展状态的相互作用, 以非线性系数为检测的 c =E / ( 5 )
ρ
声学参数, 分析非线性系数与应力的关系。文章实 因此式( 3 ) 也可表示为
现了非线性超声谐波检测技术对混凝土应力状态的 ∂u 2 ∂u ∂u∂u
2
2
2
2 = c ∂x 2 + β ∂x∂x ( 6 )
有效检测, 为非线性参数谐波技术应力检测的定量 ∂t 2
表征提供了参考。 设式( 4 ) 的初始条件为

u ( 0 , t ) =A 0 sinωt ( 7 )
1 非线性超声谐波应力检测方法
式中: A 0 为初始振幅; ω 为角频率。
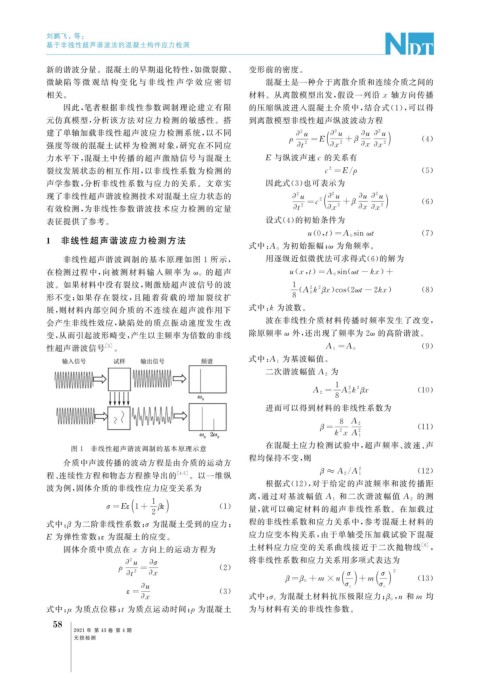
非线性超声谐波调制的基本原理如图 1 所示, 用逐级近似微扰法可求得式( 6 ) 的解为
的超声
在检测过程中, 向被测材料输入频率为 ω 0 u ( x , t ) =A 0 sin ( ωt-kx ) +
波。如果材料中没有裂纹, 则激励超声波信号的波 1
2 2
( A 0 k β x ) cos ( 2ωt-2 kx ) ( 8 )
形不变; 如果存在裂纹, 且随着荷载的增加 裂纹扩 8
展, 则材料内部空间介质的不连续在超声波作用下 式中: k 为波数。
会产生非线性效应, 缺陷处的质点振动速度发生改 波在非线性介质材料传播时频率发生了改变,
变, 从而引起波形畸变, 产生以主频率为倍数的非线 除原频率ω 外, 还出现了频率为 2 ω 的高阶谐波。
性超声谐波信号 [ 3 ] 。 A 1 =A 0 ( 9 )
为基波幅值。
式中: A 1
为
二次谐波幅值 A 2
1
A 2 = A 0 k β x ( 10 )
2 2
8
进而可以得到材料的非线性系数为
8 A 2
β= 2 2 ( 11 )
kx A 1
图 1 非线性超声谐波调制的基本原理示意 在混凝土应力检测试验中, 超声频率、 波速、 声
程均保持不变, 则
介质中声波传播的波动方程是由介质的运动方
2
/ ( 12 )
程、 连续性方程和物态方程推导出的 [ 4-5 ] 。以一维纵 β ≈ A 2 A 1
根据式( 12 ), 对于给定的声波频率和波传播距
波为例, 固体介质的非线性应力应变关系为
的测
离, 通过对基波幅值 A 1 和二次谐波幅值 A 2
1
σ=Eε 1+ β ε ( 1 ) 量, 就可以确定材料的超声非线性系数。在加载过
2

程的非线性系数和应力关系中, 参考混凝土材料的
式中: 为二阶非线性系数; σ 为混凝土受到的应力;
β
应力应变本构关系, 由于单轴受压加载试验下混凝
E 为弹性常数; ε 为混凝土的应变。
固体介质中质点在x 方向上的运动方程为 土材料应力应变的关系曲线接近于二次抛物线 [ 6 ] ,
2
∂u ∂ σ 将非线性系数和应力关系用多项式表达为
ρ 2 = ( 2 )
∂t ∂x σ σ 2
+m
β= β 0 +m ×n ( 13 )
∂u σ c σ c
ε= ( 3 )
∂x 式中: σ c 为混凝土材料抗压极限应力; , n 和 m 均
β 0
式中: 为质点位移; t 为质点运动时间; 为混凝土 为与材料有关的非线性参数。
μ
ρ
8
5

2021 年 第 43 卷 第 4 期

无损检测