Page 95 - 无损检测2021年第四期

王安泉, 等:

基于曲面拟合的脉冲涡流测厚方法

信号晚期斜率与被测管道壁厚有着一一对 应的关 响应影响的叠加。图 5 为单一激励频率下的脉冲涡
系, 因此晚期信号斜率可以作为管道壁厚检测的特 流检测等效电路 [ 11 ] , 由基尔霍夫定律可知
征量, 以用来进行壁厚的反演。 I 1 R 1 +I 1 j 2π f L 1 -I 2 j 2π f M = U
综上可知, 可以通过求取晚期斜率特征量, 来计 I 2 R 2 +I 2 j 2π f L 2 -I 1 j 2π f M = 0 ( 2 )
算管道壁厚。例如求解图 3 中 6 个不同壁厚管道的 , ,
f
式中: U 为激励电压; 为激励信号频率; R 1 L 1 I 1
感应信号晚期斜率, 可以得到晚期信号斜率与壁厚 , , 分
分别为激励线圈的电阻、 电感和电流; R 2 L 2 I 2
的对应关系( 见表 1 ), 然后建立晚期信号斜率与壁 别为被测试件中感应的电阻、 电感和电流; M 为激
厚之间的关系曲线( 见图 4 )。 励线圈与被测试件之间的互感系数。
表 1 晚期信号斜率与壁厚的关系
晚期信号斜率 晚期信号斜率
管道壁厚 / mm 管道壁厚 / mm
12.0 -89.7 7.5 -187
10.5 -115.1 6.0 -279
9.0 -135 4.5 -365
图 5 单一激励频率下的脉冲涡流检测等效电路
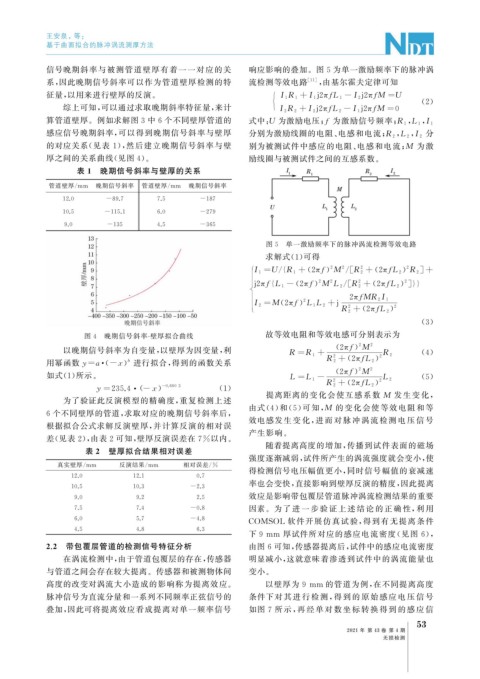
求解式( 1 ) 可得
2
2
I 1 = U /{ R 1 + 2π f M /[ R 2 + 2π f L 2 R 2 +
( ) 2 2 ( ) ]
2
2
{ ( ) 2 /[ 2 ( )]}}

j 2π f L 1 - 2π f M L 2 R 2 + 2π f L 2

2π f MR 2 I 1
2
)
I 2 =M ( 2π f L 1 L 2 + j
2
2
(
R 2 + 2π f L 2 )

( 3 )
图 4 晚期信号斜率 - 壁厚拟合曲线 故等效电阻和等效电感可分别表示为
2
)
以晚期信号斜率为自变量, 以壁厚为因变量, 利 R =R 1 + ( 2π f M 2 ( 4 )
2
2 ( ) R 2
用幂函数 y=a ·( -x ) 进行拟合, 得到的函数关系 R 2 + 2π f L 2
b
2
( 2π f M 2
)
如式( 1 ) 所示。 L =L 1 - ( 5 )
2 2 L 2
(
R 2 + 2π f L 2 )
-x )
y= 235.4 ·( - 0.6603 ( 1 )
提离距离的变化会使互感系数 M 发生变化,
为了验证此反演模型的精确度, 重复检测上述
由式( 4 ) 和( 5 ) 可知, M 的变化会使等效电阻 和 等
6 个不同壁厚的管道, 求取对应的晚期信号斜率后,
效电感发 生 变 化, 进 而 对 脉 冲 涡 流 检 测 电 压 信 号
根据拟合公式求解反演壁厚, 并计算反演的相对误
产生影响。
差( 见表 2 ), 由表 2 可知, 壁厚反演误差在 7% 以内。
随着提离高度的增加, 传播到试件表面的磁场
表 2 壁厚拟合结果相对误差
强度逐渐减弱, 试件所产生的涡流强度就会变小, 使
真实壁厚 / mm 反演结果 / mm 相对误差 / %
得检测信号电压幅值更小, 同时信号幅值的衰减速
12.0 12.1 0.7
率也会变快, 直接影响到壁厚反演的精度, 因此提离
10.5 10.3 -2.3
效应是影响带包覆层管道脉冲涡流检测结果的重要
9.0 9.2 2.5
7.5 7.4 -0.8 因素。为 了 进 一 步 验 证 上 述 结 论 的 正 确 性, 利 用
COMSOL 软件开展仿真试验, 得到有无提离条件
6.0 5.7 -4.8
4.5 4.8 6.3
下 9mm 厚试件所对应的感应电流密度( 见图 6 ),
2.2 带包覆层管道的检测信号特征分析 由图 6 可知, 传感器提离后, 试件中的感应电流密度
在涡流检测中, 由于管道包覆层的存在, 传感器 明显减小, 这就意味着渗透到试件中的涡流能量也
与管道之间会存在较大提离。传感器和被测物体间 变小。

高度的改变对涡流大小造成的影响称为提离效应。 以壁厚为 9mm 的管道为例, 在不同提离高度
脉冲信号为直流分量和一系列不同频率正弦信号的 条件下对 其 进 行 检 测, 得 到 的 原 始 感 应 电 压 信 号
叠加, 因此可将提离效应看成提离对单一频率信号 如图 7 所 示, 再 经 单 对 数 坐 标 转 换 得 到 的 感 应 信
3
5
2021 年 第 43 卷 第 4 期

无损检测