Page 52 - 无损检测2025年第二期

李爱华，等：

陶瓷基黏接件超声检测缺陷信号的处理方法

号进行小波分解，得到不同尺度上的小波系数。 5
软阈值
（3）对 小 波 系数进行阈值处理。选择合适 4 硬阈值

的阈值，将小于阈值的系数设为 0（通常被认为是 3 笔者所提改进阈值方法
孙万麟改进阈值函数(文献16)
噪声信号），保留大于阈值的系数（通常被认为是 2 1 刘冲改进阈值函数(文献17)
有效信号）。常用的阈值处理方法为硬阈值和软 阈值化后的小波系数 0
阈值。 -1
（4）使用处理后的小波系数进行小波逆变 -2

换，将处理后的系数重建为去噪后的信号。 -3
-4
1.3 改进的阈值处理方法
-5
在对小波系数进行阈值处理时，传统方法有硬 -5 0 5
小波系数
阈值处理和软阈值处理两种。
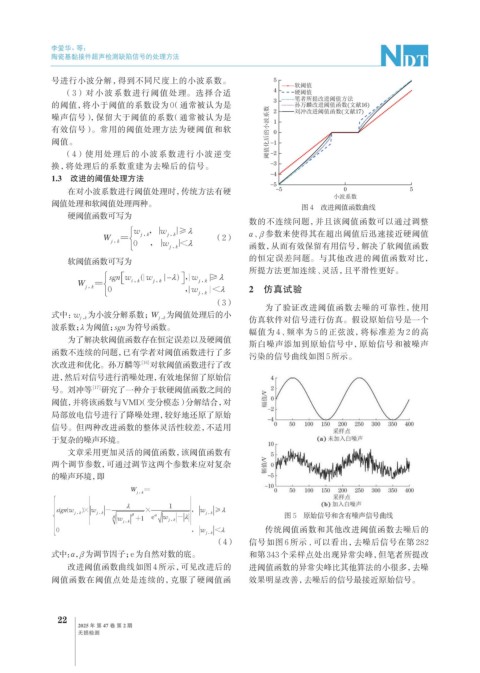
图 4 改进阈值函数曲线
硬阈值函数可写为
数的不连续问题，并且该阈值函数可以通过调整

（2） α、 β 参数来使得其在超出阈值后迅速接近硬阈值
函数，从而有效保留有用信号，解决了软阈值函数
软阈值函数可写为 的恒定误差问题。与其他改进的阈值函数对比，
所提方法更加连续、灵活，且平滑性更好。

2 仿真试验
（3）
为了验证改进阈值函数去噪的可靠性，使用
式中：w 为小波分解系数；W 为阈值处理后的小 仿真软件对信号进行仿真。假设原始信号是一个
j，k
j，k
波系数； λ为阈值； sgn为符号函数。
幅值为 4、 频率为 5 的正弦波，将标准差为 2 的高
为了解决软阈值函数存在恒定误差以及硬阈值
斯白噪声添加到原始信号中，原始信号和被噪声
函数不连续的问题，已有学者对阈值函数进行了多
污染的信号曲线如图 5 所示。
次改进和优化。孙万麟等 [16] 对软阈值函数进行了改
进，然后对信号进行消噪处理，有效地保留了原始信
号。刘冲等 [17] 研究了一种介于软硬阈值函数之间的
阈值，并将该函数与VMD（变分模态）分解结合，对
局部放电信号进行了降噪处理，较好地还原了原始
信号。但两种改进函数的整体灵活性较差，不适用
于复杂的噪声环境。
文章采用更加灵活的阈值函数，该阈值函数有
两个调节参数，可通过调节这两个参数来应对复杂
的噪声环境，即

图 5 原始信号和含有噪声信号曲线
传统阈值函数和其他改进阈值函数去噪后的
（4） 信号如图 6 所示 , 可以看出，去噪后信号在第 282
式中： α， β为调节因子；e为自然对数的底。 和第 343 个采样点处出现异常尖峰，但笔者所提改
改进阈值函数曲线如图 4 所示， 可见改进后的 进阈值函数的异常尖峰比其他算法的小很多，去噪
阈值函数在阈值点处是连续的，克服了硬阈值函 效果明显改善，去噪后的信号最接近原始信号。

22
2025 年 第 47 卷 第 2 期
无损检测