Page 79 - 无损检测2024年第四期

张恒熙,等:
444 铁磁性不锈钢焊管缺陷的识别与分类

多有效信息, 笔者计算原信号 x ( t )与各阶 IMF 分 子。选取的频域参数分别为: 重心频率, 均方频率,
量之间的互相关系数, 其结果如表 3 所示, 可以看 均方根频率, 频率方差, 频率标准差。提取每条涡流
()
()
()
()
出, c 1 t ~c 5 t 互相关系数较大, 为了减少数据 信号c 1 t ~c 5 t 的 16 个特征参数, 即每条信号
()
冗余, 各缺陷信号将通过c 1 t ~c 5 t 来表示。 共有 80 个特征参数。
()
表 3 各阶IMF 分量的互相关系数

()
()
()
缺陷情况 c 1 t () c 3 t () c 5 t c 6 t ~c 9 t
() c 2 t
() c 4 t
通孔 0.033 0.282 0.549 0.639 0.571 <0.1
裂纹 0.310 0.929 0.840 0.397 0.115 <0.1
正常 0.249 0.498 0.601 0.471 0.213 <0.1
平均 0.197 0.569 0.663 0.502 0.299 <0.1
3.3 特征参数降维
由于试验选取的缺陷信号特征参数较多, 这些
特征参数间不可避免地会存在一定的相关性, 导致
信息的重复。同时为了降低问题的复杂性、 提高后
期识别效率, 采用主成分分析方法( PCA ) 对特征参
数降维 [ 9 ] 。 PCA 的基本思想是对原数据进行重组,
得到一组新的互不相关且相互独立的数据, 来达到
以较少的数据表现原始数据特征信息的目的 [ 10-11 ] 。
设为 85% 。经 PCA 处
试验将累计贡献率 C m
理后的主成分贡献率变化曲线如图 7 所示, 可以看
出, 经过 PCA 处理后, 原信号的80 个特征参数最终
简化为 12 个特征参数。
4 基于 SVM 的分类模型训练

[ 12 ]
支持向量机( SVM ) 是一种二分类算法, 较多
应用在小样本分类问题上。其原理是寻找一个满足
分类要求的最优分类超平面, 使得该超平面在保证
分类精度的同时, 能够使超平面两侧的空白区域最
大化 [ 13-14 ] 。
在使用 SVM 分类过程中选择合适的核函数是
较为关键的一步, 核函数的作用是在高维特征空间
中找到一个最佳的线性分类超平面( 可通过计算特
征空间中的向量与支持向量的内积来实现), 这样就
可将输入空间中的非线性分类问题转换为高维特征
空间中的线性分类问题 [ 15 ] 。通过比较发现, 相较于
其他核函数, 径向基核函数( RBF ) 的参数较少, 可以
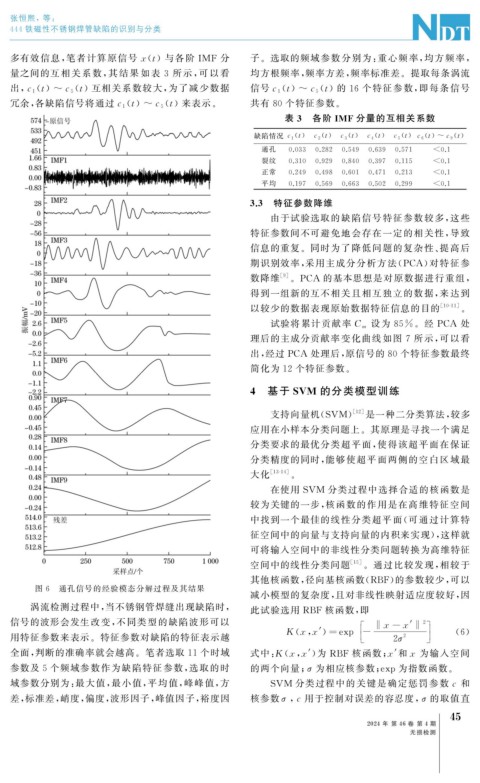
图 6 通孔信号的经验模态分解过程及其结果
减小模型的复杂度, 且对非线性映射适应度较好, 因
涡流检测过程中, 当不锈钢管焊缝出现缺陷时, 此试验选用 RBF 核函数, 即
信号的波形会发生改变, 不同类型的缺陷波形可以
‖x -x'‖
=
用特征参数来表示。特征参数对缺陷的特征表示越 K ( x , x' ) ex p - 2σ 2 ( 6 )
2

全面, 判断的准确率就会越高。笔者选取 11 个时域 式中: K ( x , x' ) 为 RBF 核函数; x'和x 为输入空间
参数及 5 个频域参数作为缺陷特征参数, 选取的时 的两个向量; σ 为相应核参数; ex p 为指数函数。
域参数分别为: 最大值, 最小值, 平均值, 峰峰值, 方 SVM 分类过程中的关键是确定惩罚参数c 和
差, 标准差, 峭度, 偏度, 波形因子, 峰值因子, 裕度因 核参数 σ , c 用于控制对误差的容忍度, σ 的取值直
5
4
2024 年 第 46 卷 第 4 期
无损检测