Page 73 - 无损检测2024年第四期
P. 73
程宝谊,等:
核电混凝土相控阵超声检测的数值模拟分析
在的圆的方程为x + y =10 。为得到不同发射阵 为 F 1 , 接收阵元中心为 F 2 , 超声波传播路径总长为
2
2
2
元与接收阵元的反射点, 按照所处象限不同的阵元 L , 则可得椭圆方程 F ( x , ), 即
y
将传播路径和反射点分为以下 3 种情况。 x 2 y 2
2 + 2 = 1 ( 8 )
a b
2 2 2 的距离。
式中: 2a=L ; c =a -b ; 2c 为F 1 到 F 2
类推可得每个不同传播路径的椭圆方程, 这些
椭圆方程均在反射点处与缺陷相切。则缺陷的上边
缘可以用该曲线族 F ( x , , t ) 的包络来表示。
y
图 9 声束传播路线示意
情况 ① 如图 9 中传播路线 1 所示。发射阵元和
接收阵元都位于第二象限中。
情况 ② 如图 9 中传播路线 2 所示。与情况 ① 的
差别仅是象限不同, 但其发射阵元与接收阵元均在
同一象限即第一象限中。 图 11 流程 A 声束传播路线示意
情况 ③ 较为复杂, 发射阵元与接收阵元处于不 4.3 声束偏转角度对混凝土缺陷检测的影响
同象限中, 如图 9 中传播路线 3 所示。 此次验证试验的缺陷位于阵列中点偏右位置。
试 验 测 得 波 在 混 凝 土 中 的 传 播 声 速 为 为了验证不同声束偏转角度对混凝土缺陷检测的影
-1
3571m · s , 则根据几何关系计算得到 63.96 μ s 响, 将偏转角分别设置为 0° , 15° , 30° , 45° 进行模拟
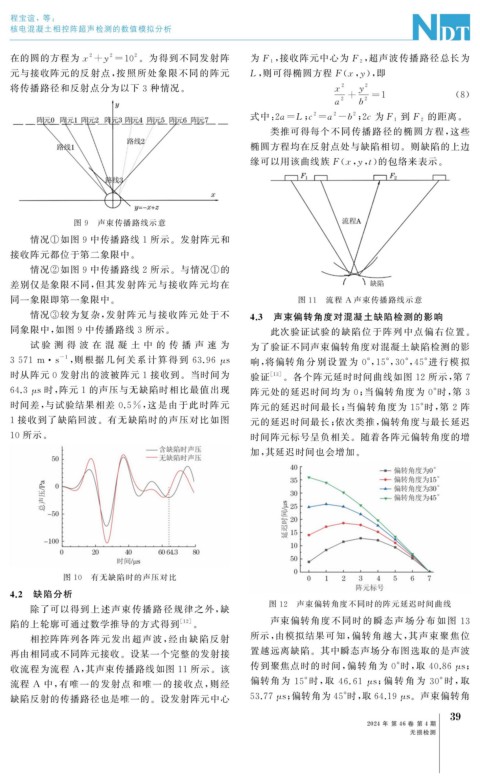
时从阵元 0 发射出的波被阵元 1 接收到。当时间为 验证 [ 13 ] 。各个阵元延时时间曲线如图 12 所示, 第 7
64.3 μ s时, 阵元 1 的声压与无缺陷时相比最值出现 阵元处的延迟时间均为 0 ; 当偏转角度为 0° 时, 第 3
时间差, 与试验结果相差 0.5% , 这是由于此时阵元 阵元的延迟时间最长; 当偏转角度为 15° 时, 第 2 阵
1 接收到了缺陷回波。有无缺陷时的声压对比如图 元的延迟时间最长; 依次类推, 偏转角度与最长延迟
10 所示。 时间阵元标号呈负相关。随着各阵元偏转角度的增
加, 其延迟时间也会增加。
图 10 有无缺陷时的声压对比
4.2 缺陷分析
图 12 声束偏转角度不同时的阵元延迟时间曲线
除了可以得到上述声束传播路径规律之外, 缺
陷的上轮廓可通过数学推导的方式得到 [ 12 ] 。 声束偏转角度不同时的瞬态声场分布如图 13
相控阵阵列各阵元发出超声波, 经由缺陷反射 所示, 由模拟结果可知, 偏转角越大, 其声束聚焦位
再由相同或不同阵元接收。设某一个完整的发射接 置越远离缺陷。其中瞬态声场分布图选取的是声波
收流程为流程 A , 其声束传播路线如图 11 所示。该 传到聚焦点时的时间, 偏转角为 0° 时, 取 40.86 μ s ;
流程 A 中, 有唯一的发射点和唯一的接收点, 则经 偏转角为 15° 时, 取 46.61 μ s ; 偏 转 角 为 30° 时, 取
缺陷反射的传播路径也是唯一的。设发射阵元中心 53.77 μ s ; 偏转角为45° 时, 取64.19 μ s 。声束偏转角
9
3
2024 年 第 46 卷 第 4 期
无损检测